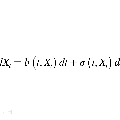We present an error analysis of weak convergence of one-step numerical schemes for stochastic differential equations (SDEs) with super-linearly growing coefficients. Following Milstein's weak error analysis on the one-step approximation of SDEs, we prove a general conclusion on weak convergence of the one-step discretization of the SDEs mentioned above. As applications, we show the weak convergence rates for several numerical schemes of half-order strong convergence, such as tamed and balanced schemes. Numerical examples are presented to verify our theoretical analysis.
翻译:我们提出一种针对具有超线性增长系数的随机微分方程(SDEs)一步数值方案的弱收敛误差分析。在继承了Milstein对SDEs一步逼近方法的弱误差分析的基础上,我们证明了对于上述SDEs的一步离散化的一般弱收敛结果。作为应用,我们展示了超过半阶强收敛的几种数值方案的弱收敛率,例如平衡方案和平滑方案。我们还给出了数值例子验证了理论分析的正确性。