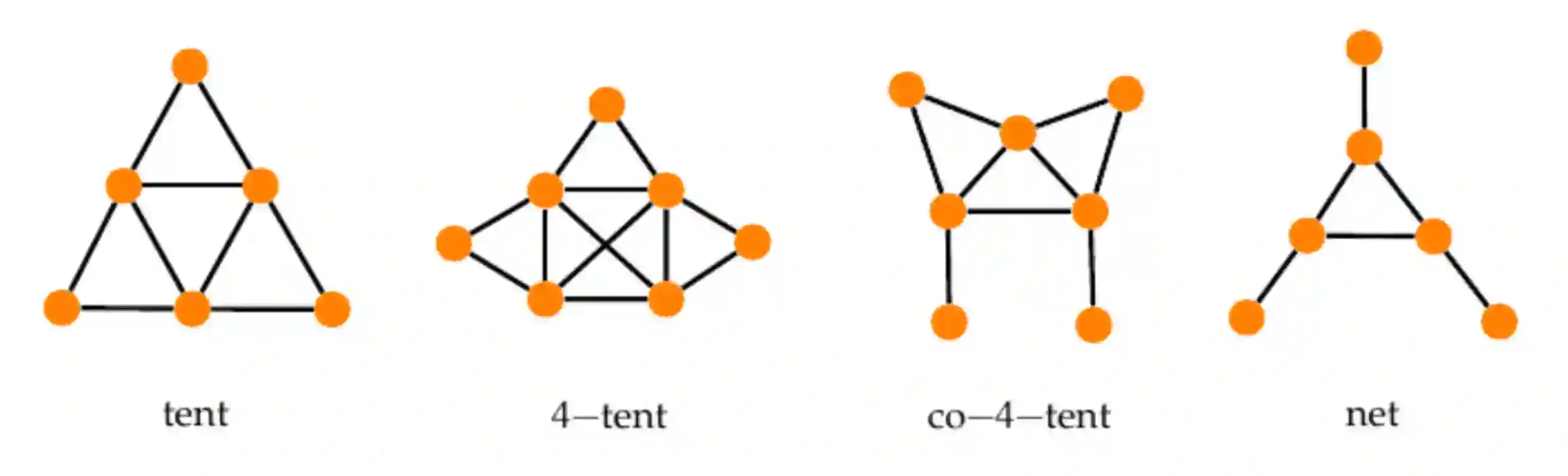
A $(0,1)$-matrix has the consecutive-ones property (C1P) if its columns can be permuted to make the $1$'s in each row appear consecutively. This property was characterised in terms of forbidden submatrices by Tucker in 1972. Several graph classes were characterised by means of this property, including interval graphs and strongly chordal digraphs. In this work, we define and characterise 2-nested matrices, which are $(0,1)$-matrices with a variant of the C1P and for which there is also certain assignment of one of two colors to each block of consecutive $1$'s in each row. The characterization of 2-nested matrices in the present work is of key importance to characterise split graphs that are also circle by minimal forbidden induced subgraphs.
翻译:A(0,1,1美元)矩阵具有连续的属性(C1P),如果其列可以排列,使每行的1美元连续出现。该属性由1972年塔克用被禁止的次矩阵来定性。一些图形类别用该属性来定性,包括间距图和强烈的光谱。在这项工作中,我们用C1P的变量来定义和描述2个正弦矩阵($(0,1美元)-矩阵),这些矩阵与C1P的变量是1美元(0,1美元)-矩阵,对于每个行的连续1美元每个块也指定了2种颜色之一。目前工作中对2个正弦矩阵的定性对于通过最小的禁止诱导子图来区分圆形的分裂图具有关键重要性。