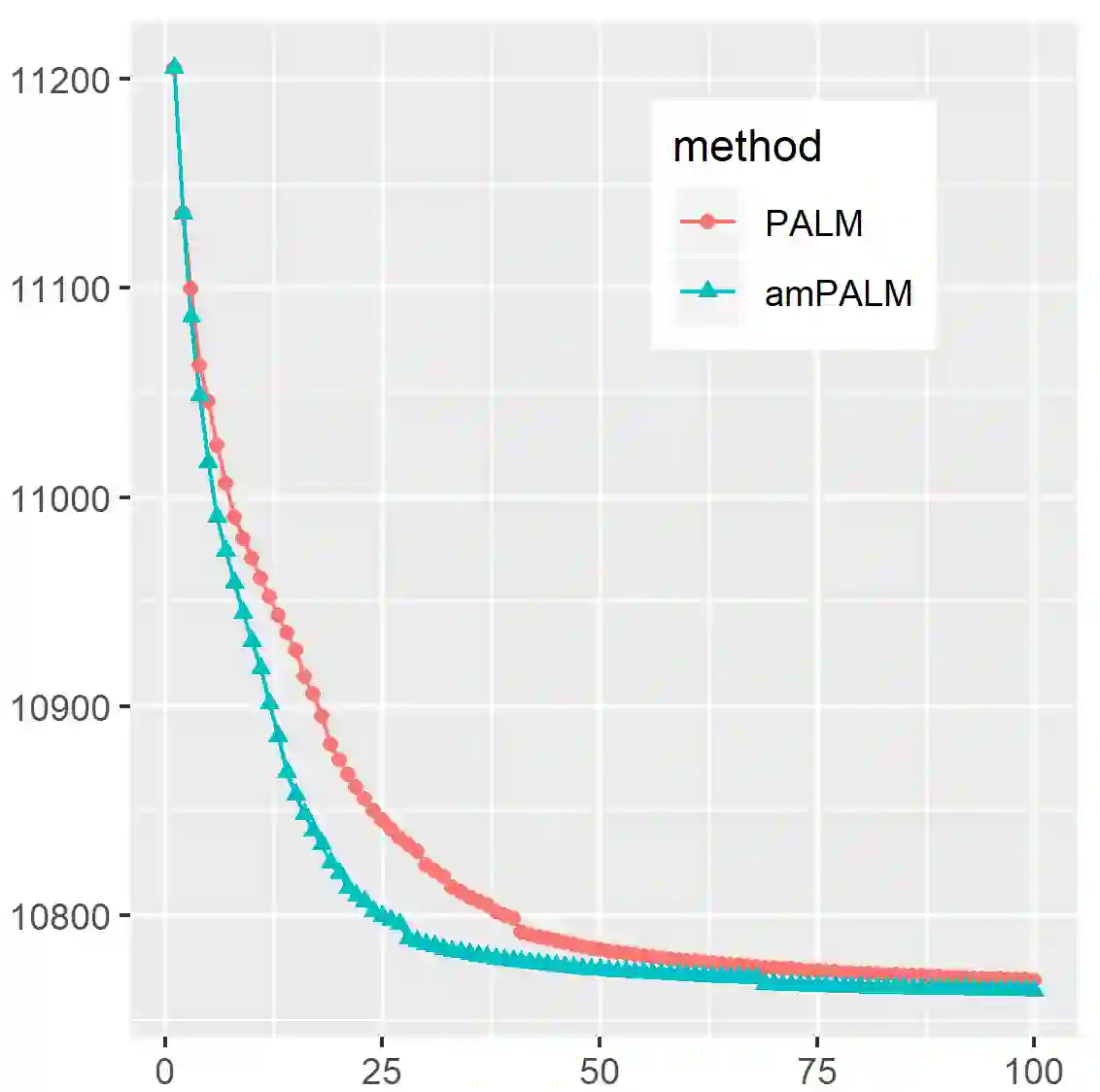
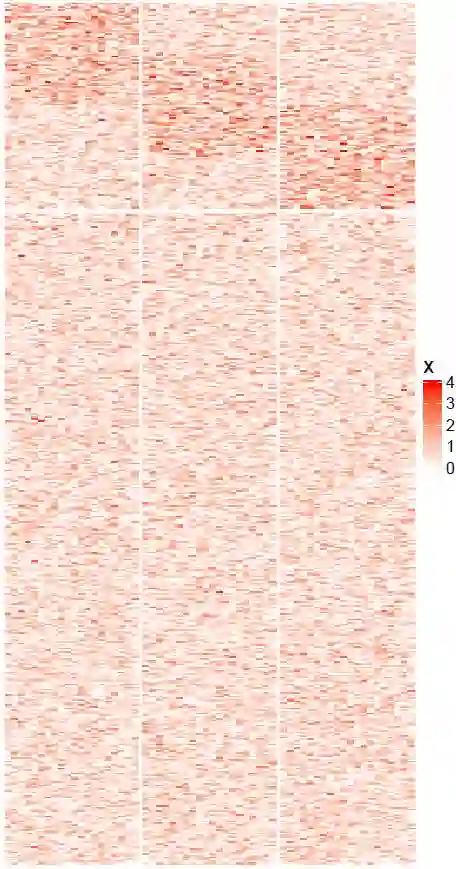
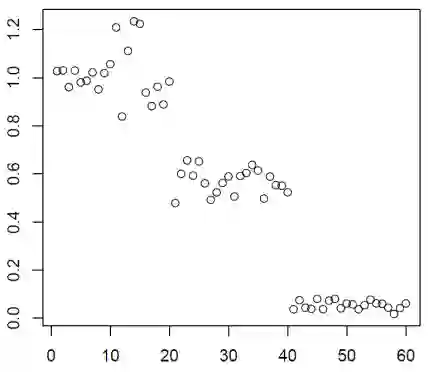
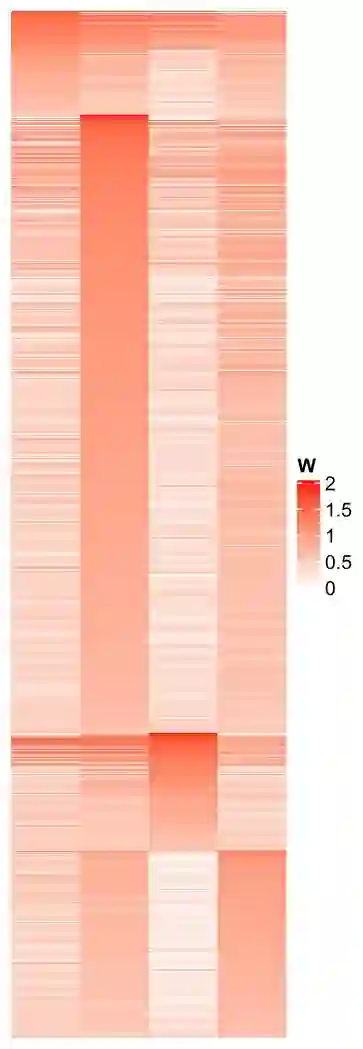
Non-negative matrix factorization (NMF) is a powerful tool for dimensionality reduction and clustering. Unfortunately, the interpretation of the clustering results from NMF is difficult, especially for the high-dimensional biological data without effective feature selection. In this paper, we first introduce a row-sparse NMF with $\ell_{2,0}$-norm constraint (NMF_$\ell_{20}$), where the basis matrix $W$ is constrained by the $\ell_{2,0}$-norm, such that $W$ has a row-sparsity pattern with feature selection. It is a challenge to solve the model, because the $\ell_{2,0}$-norm is non-convex and non-smooth. Fortunately, we prove that the $\ell_{2,0}$-norm satisfies the Kurdyka-\L{ojasiewicz} property. Based on the finding, we present a proximal alternating linearized minimization algorithm and its monotone accelerated version to solve the NMF_$\ell_{20}$ model. In addition, we also present a orthogonal NMF with $\ell_{2,0}$-norm constraint (ONMF_$\ell_{20}$) to enhance the clustering performance by using a non-negative orthogonal constraint. We propose an efficient algorithm to solve ONMF_$\ell_{20}$ by transforming it into a series of constrained and penalized matrix factorization problems. The results on numerical and scRNA-seq datasets demonstrate the efficiency of our methods in comparison with existing methods.
翻译:非负矩阵因子化(NMF)是维度减少和组合的强大工具。 不幸的是, 国家MF对组群结果的解释非常困难, 特别是对于高维生物数据而言, 没有有效的特性选择 。 在本文中, 我们首先引入了以$\ ell\\2, 0}$- 诺姆限制( NMF_ $\\\\\\ ell\ ⁇ 20} $- 诺姆限制 (NMF_ $_ =2, 0} $- 美元) 的行扭曲 NMF 的组合结果很难解释。 很遗憾, 特别是对于高维生物数据, 特别是高维生物数据。 幸运的是, 我们证明, 美元- 诺米克- 美元基质约束 受美元 的基质交替线性最小最小化算法及其在特性选择的单质化模式上 解决 NMFF_ $\ =20} 模型是一个挑战, 因为 美元 诺尔- 诺尔- 的内基数据 的稳定性 质化方法, 我们目前使用SMFal_ ral_ ral_ ral_ ral_ ral_ ral_ ral_ ral_ exx roupal_ yal_ roupal_ roupal_ roupal_ roupal_ yal_ roupal_ a roupal_ a roup romax rouptal_ roup roup rouption rouptional_ rod_ rod_ roupd_ rod_ roup rod rod rod_ rod_ roc_ rod roc_ a rodal_ rod rodal_ rodal_ rodal_ rodal_ ycal_ rocal_ rocal_ rod rod rod_ rod rod rod_ rod rod rod_ rod_ rod_ rocal_ rocisal_ roup rocal_ roup