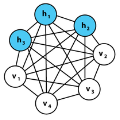
A restricted Boltzmann machine (RBM) is an undirected graphical model constructed for discrete or continuous random variables, with two layers, one hidden and one visible, and no conditional dependency within a layer. In recent years, RBMs have risen to prominence due to their connection to deep learning. By treating a hidden layer of one RBM as the visible layer in a second RBM, a deep architecture can be created. RBMs are thought to thereby have the ability to encode very complex and rich structures in data, making them attractive for supervised learning. However, the generative behavior of RBMs is largely unexplored and typical fitting methodology does not easily allow for uncertainty quantification in addition to point estimates. In this paper, we discuss the relationship between RBM parameter specification in the binary case and model properties such as degeneracy, instability and uninterpretability. We also describe the associated difficulties that can arise with likelihood-based inference and further discuss the potential Bayes fitting of such (highly flexible) models, especially as Gibbs sampling (quasi-Bayes) methods are often advocated for the RBM model structure.
翻译:限制的Boltzmann机器(RBM)是针对离散的或连续的随机变量、两层、一层隐藏的和一层可见的、在一层内没有有条件依赖性的一种非定向的图形模型。近年来,成果管理制因其与深层学习的联系而越来越突出。通过将一个成果管理制的隐藏层作为第二个成果管理制的可见层,可以创建一个深层结构。成果管理制被认为因此有能力对非常复杂和丰富的数据结构进行编码,使其对受监督的学习具有吸引力。但是,成果管理制的遗传行为基本上没有得到探讨,而且典型的调整方法不易在点估之外进行不确定的量化。在本文件中,我们讨论了二进制案例的成果管理制参数规格与模型属性之间的关系,例如退化、不稳定和互不易性。我们还描述了在基于可能性的推断中可能出现的相关困难,并进一步讨论了这类模型(高度灵活)可能适合的海湾。特别是Gibbs抽样( quis-Bayes)方法常常被提倡用于成果管理制模型结构。