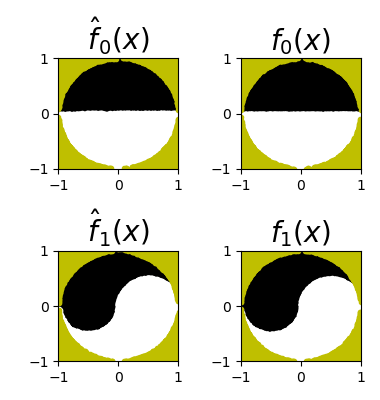
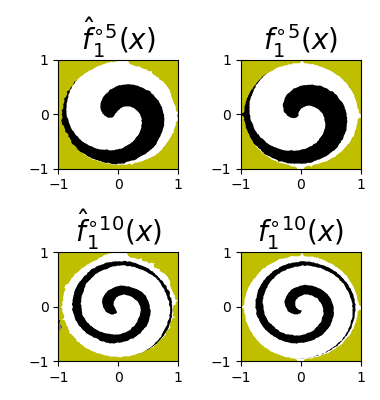
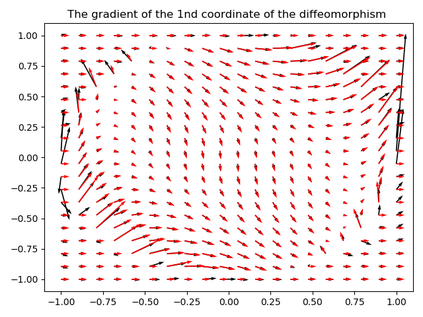
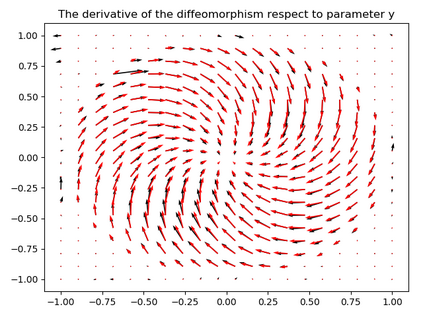
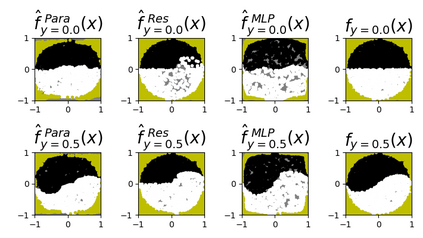
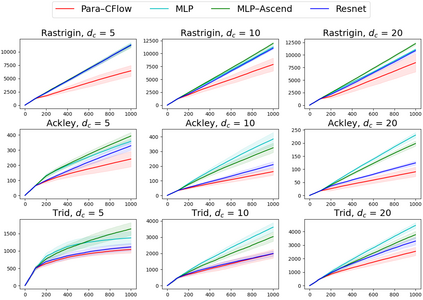
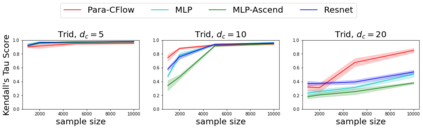
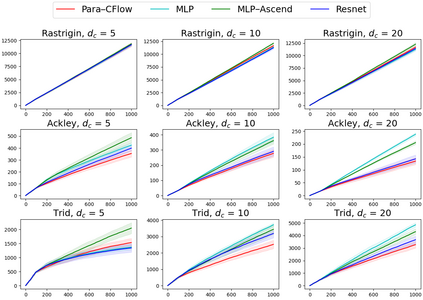
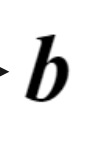Invertible neural networks based on Coupling Flows CFlows) have various applications such as image synthesis and data compression. The approximation universality for CFlows is of paramount importance to ensure the model expressiveness. In this paper, we prove that CFlows can approximate any diffeomorphism in C^k-norm if its layers can approximate certain single-coordinate transforms. Specifically, we derive that a composition of affine coupling layers and invertible linear transforms achieves this universality. Furthermore, in parametric cases where the diffeomorphism depends on some extra parameters, we prove the corresponding approximation theorems for our proposed parametric coupling flows named Para-CFlows. In practice, we apply Para-CFlows as a neural surrogate model in contextual Bayesian optimization tasks, to demonstrate its superiority over other neural surrogate models in terms of optimization performance.
翻译:以调合流为根据的不可逆神经网络)有各种应用,如图像合成和数据压缩等。CFlows的近似普遍性对于确保模型的表达性至关重要。在本文中,我们证明CFlows如果其层能近似某些单一坐标变异,就可以在Ck-norm 中近似任何异己形态。具体地说,我们推论,由亲和偶和线性变异组成的结构可以实现这一普遍性。此外,在对称法主义依赖某些额外参数的参数的参数的情况下,我们证明了我们提议的Para-CFlows准对准组合流的相应近近似性理论。在实践中,我们用Para-CFlows作为贝耶斯优化任务的神经外壳模型,以展示其在优化性能方面优于其他神经外壳外形模型的优势。