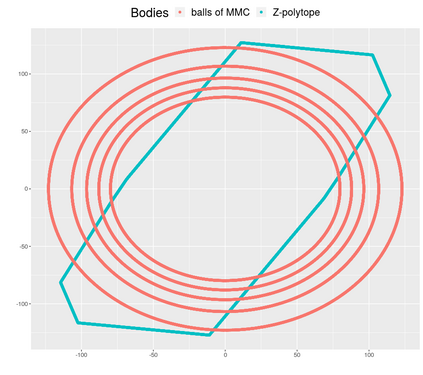
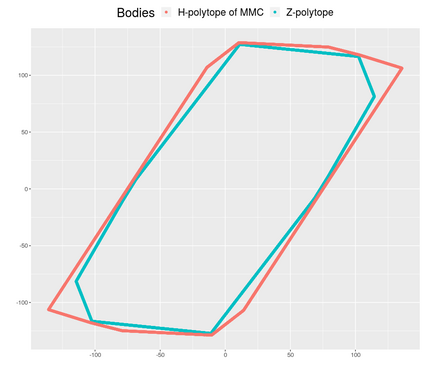
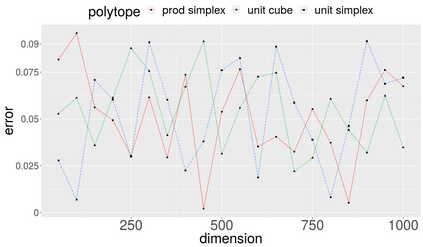
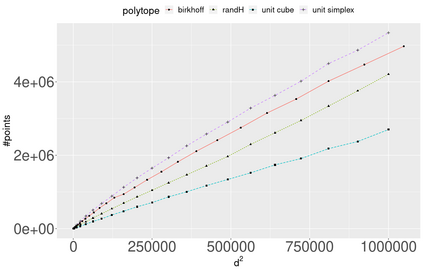
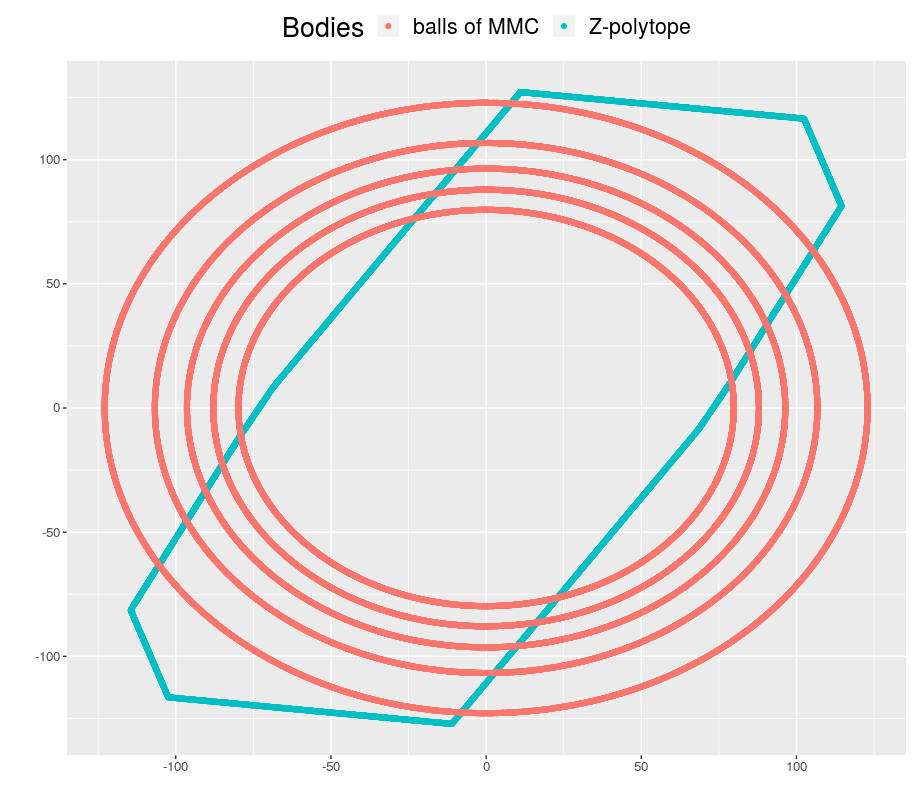
We tackle the problem of efficiently approximating the volume of convex polytopes, when these are given in three different representations: H-polytopes, which have been studied extensively, V-polytopes, and zonotopes (Z-polytopes). We design a novel practical Multiphase Monte Carlo algorithm that leverages random walks based on billiard trajectories, as well as a new empirical convergence tests and a simulated annealing schedule of adaptive convex bodies. After tuning several parameters of our proposed method, we present a detailed experimental evaluation of our tuned algorithm using a rich dataset containing Birkhoff polytopes and polytopes from structural biology. Our open-source implementation tackles problems that have been intractable so far, offering the first software to scale up in thousands of dimensions for H-polytopes and in the hundreds for V- and Z-polytopes on moderate hardware. Last, we illustrate our software in evaluating Z-polytope approximations.
翻译:我们解决了高效接近 convex 聚顶体体积的问题。 当用三种不同的表达方式给出这些表达方式:H-polytops, 已经进行了广泛研究的H-polytops, V-polytops 和 zonoopes (Z-polytops ) 。 我们设计了一个新的实用的多阶段蒙特卡洛 算法, 利用台球轨迹来利用随机行走, 以及一项新的经验趋同测试和适应性 convex 体的模拟穿透时间表。 在调整了我们拟议方法的若干参数之后, 我们用包含 Birkhoff 聚顶和 结构生物学 的聚顶点的丰富数据集, 对我们的调控算法进行了详细的实验性评估。 我们的开放源执行解决了迄今一直难以解决的问题, 提供了第一个软件, 来将H-polytops和中度硬件的 V- 和 Z-polytops 的数以千维维维维度放大。 最后, 我们用软件来评估 Z-polytope 近似 。