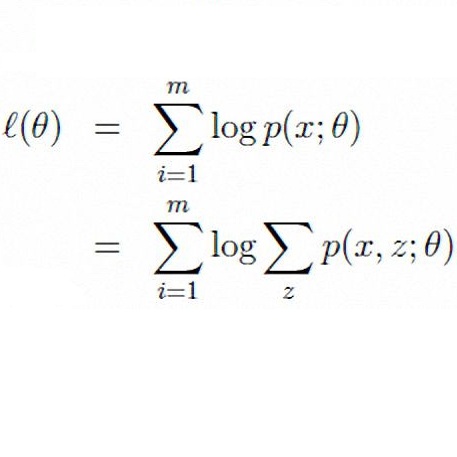Iterative minimization algorithm on mixture family

Iterative minimization algorithms appear in various areas including machine learning, neural network, and information theory. The em algorithm is one of the famous one in the former area, and Arimoto-Blahut algorithm is a typical one in the latter area. However, these two topics had been separately studied for a long time. In this paper, we generalize an algorithm that was recently proposed in the context of Arimoto-Blahut algorithm. Then, we show various convergence theorems, one of which covers the case when each iterative step is done approximately. Also, we apply this algorithm to the target problem in em algorithm, and propose its improvement. In addition, we apply it to other various problems in information theory.