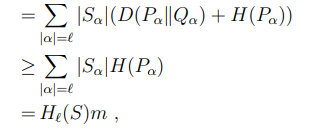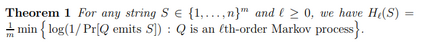Overcoming the compression limit of the individualsequence (zero order empirical entropy) using the Set Shaping Theory

Given the importance of the claim, we want to start by exposing the following consideration: this claim comes out more than a year after the article "Practical applications of Set Shaping Theory in Huffman coding" which reports the program that carried out an experiment of data compression in which the coding limit NH0(S) of a single sequence was questioned. We waited so long because, before making a claim of this type, we wanted to be sure of the consistency of the result. All this time the program has always been public; anyone could download it, modify it and independently obtain the reported results. In this period there have been many information theory experts who have tested the program and agreed to help us, we thank these people for the time dedicated to us and their precious advice. Given a sequence S of random variables i.i.d. with symbols belonging to an alphabet A; the parameter NH0(S) (the zero-order empirical entropy multiplied by the length of the sequence) is considered the average coding limit of the symbols of the sequence S through a uniquely decipherable and instantaneous code. Our experiment that calls into question this limit is the following: a sequence S is generated in a random and uniform way, the value NH0(S) is calculated, the sequence S is transformed into a new sequence f(S), longer but with the symbols belonging to the same alphabet, finally we code f(S) using Huffman coding. By generating a statistically significant number of sequences we obtain that the average value of the length of the encoded sequence f(S) is less than the average value of NH0(S). In this way, a result is obtained which is incompatible with the meaning given to NH0(S).