Splitting-off in Hypergraphs

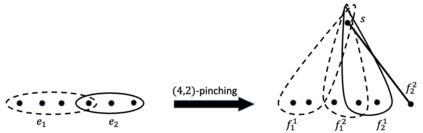
The splitting-off operation in undirected graphs is a fundamental reduction operation that detaches all edges incident to a given vertex and adds new edges between the neighbors of that vertex while preserving their degrees. Lov\'asz (1974) and Mader (1978) showed the existence of this operation while preserving global and local connectivities respectively in graphs under certain conditions. These results have far-reaching applications in graph algorithms literature. In this work, we introduce a splitting-off operation in hypergraphs. We show that there exists a local connectivity preserving complete splitting-off in hypergraphs and give a strongly polynomial-time algorithm to compute it in weighted hypergraphs. We illustrate the usefulness of our splitting-off operation in hypergraphs by showing two applications: (1) we give a constructive characterization of $k$-hyperedge-connected hypergraphs and (2) we give an alternate proof of an approximate min-max relation for max Steiner rooted-connected orientation of graphs and hypergraphs (due to Kir\'aly and Lau (Journal of Combinatorial Theory, 2008; FOCS 2006)). Our proof of the approximate min-max relation for graphs circumvents the Nash-Williams' strong orientation theorem and uses tools developed for hypergraphs.