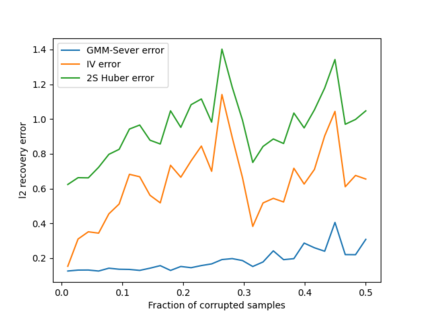
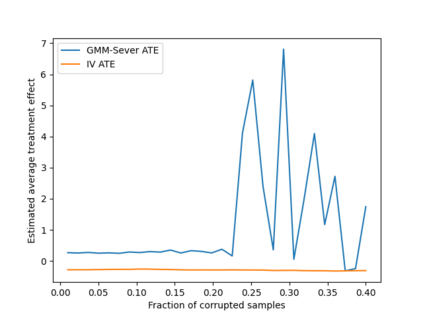
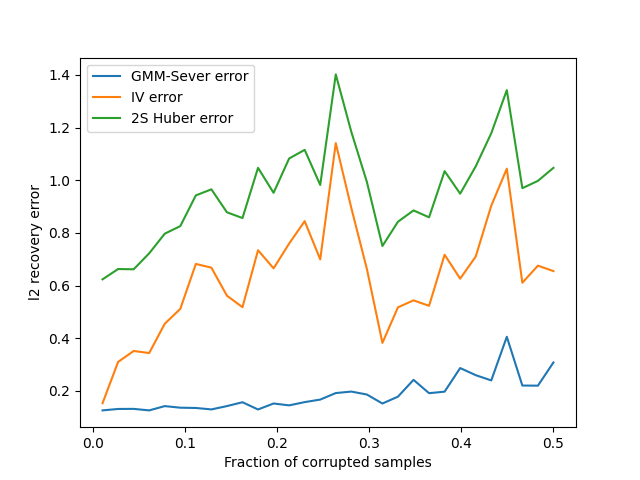
For many inference problems in statistics and econometrics, the unknown parameter is identified by a set of moment conditions. A generic method of solving moment conditions is the Generalized Method of Moments (GMM). However, classical GMM estimation is potentially very sensitive to outliers. Robustified GMM estimators have been developed in the past, but suffer from several drawbacks: computational intractability, poor dimension-dependence, and no quantitative recovery guarantees in the presence of a constant fraction of outliers. In this work, we develop the first computationally efficient GMM estimator (under intuitive assumptions) that can tolerate a constant $\epsilon$ fraction of adversarially corrupted samples, and that has an $\ell_2$ recovery guarantee of $O(\sqrt{\epsilon})$. To achieve this, we draw upon and extend a recent line of work on algorithmic robust statistics for related but simpler problems such as mean estimation, linear regression and stochastic optimization. As two examples of the generality of our algorithm, we show how our estimation algorithm and assumptions apply to instrumental variables linear and logistic regression. Moreover, we experimentally validate that our estimator outperforms classical IV regression and two-stage Huber regression on synthetic and semi-synthetic datasets with corruption.
翻译:对于统计和计量经济学中的许多推论问题,未知的参数是由一组时刻条件确定的。解决瞬间条件的通用方法是通用模型(GMM)。然而,古典的GMM估计可能非常敏感。过去曾开发过强效的GMM估计器,但有以下几个缺点:计算可忽略性、维度依赖性差,以及当有一定比例的外差时,没有量化的恢复保障。在这项工作中,我们开发了第一个计算高效的GMM估计器(根据直观假设),它可以容忍对称腐蚀性样品中固定的 $\ epslon 部分,并且具有$O(sqrt=epsilon}) 的恢复保证。为了实现这一点,我们利用并扩展了最近有关算法稳健统计的系列工作,例如平均估计、线性回归和透视优化。作为我们算法的一般的两个例子,我们展示了我们的估测算法和正反正轨数据,我们如何运用了两度的实验室级级的回归。