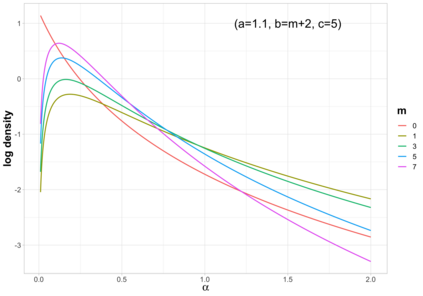
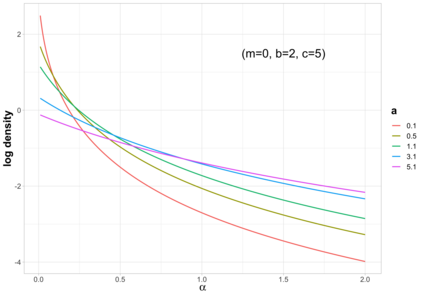
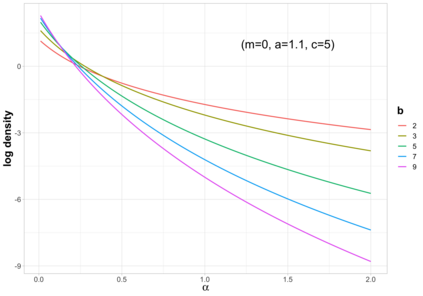
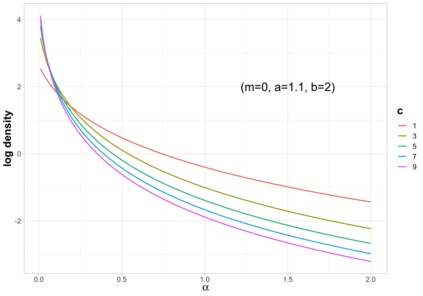
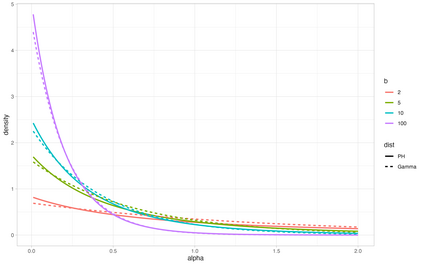
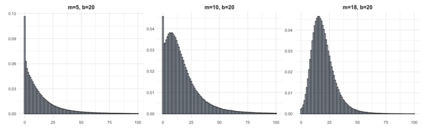
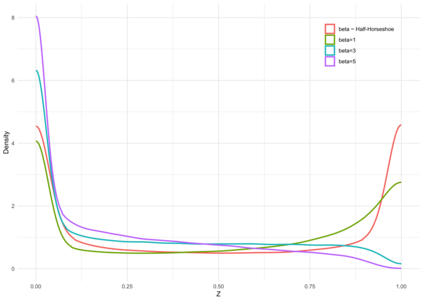
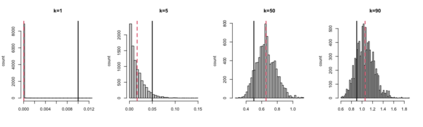
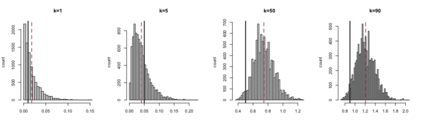
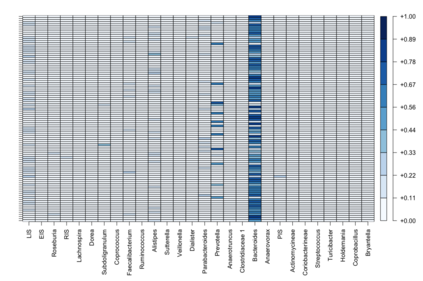
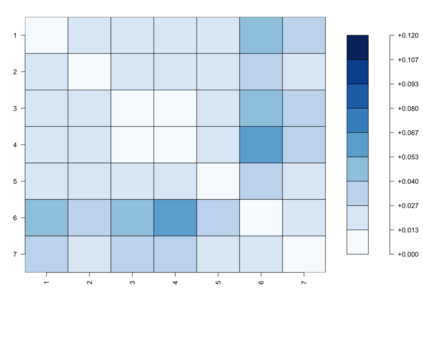
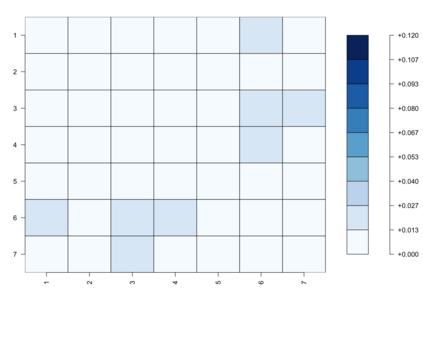
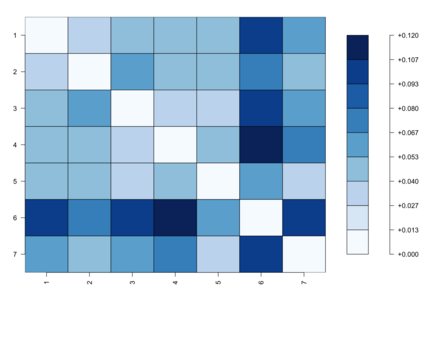
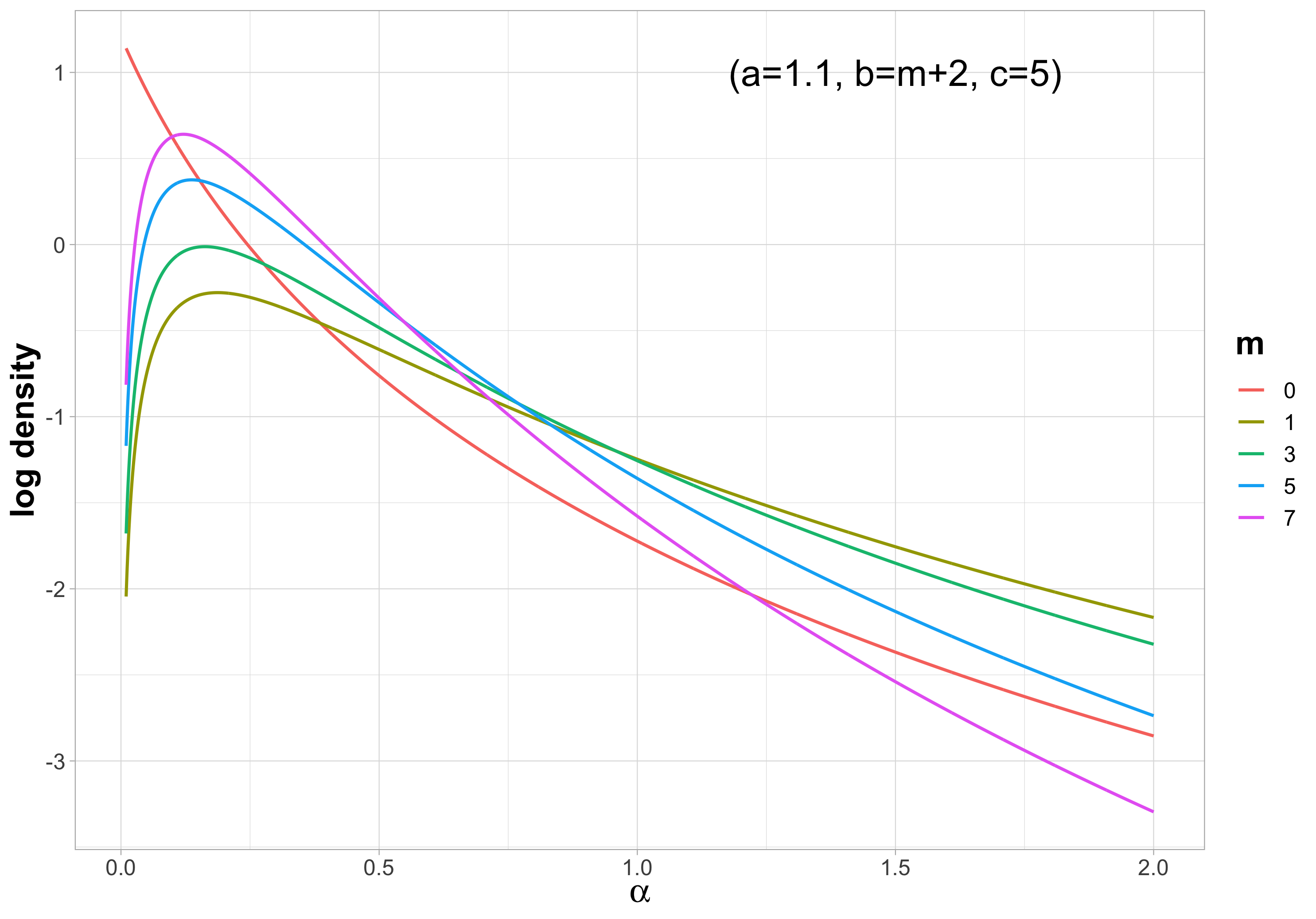
Bayesian hierarchical models are commonly employed for inference in count datasets, as they account for multiple levels of variation by incorporating prior distributions for parameters at different levels. Examples include Beta-Binomial, Negative-Binomial (NB), Dirichlet-Multinomial (DM) distributions. In this paper, we address two crucial challenges that arise in various Bayesian count models: inference for the concentration parameter in the ratio of Gamma functions and the inability of these models to effectively handle excessive zeros and small nonzero counts. We propose a novel class of prior distributions that facilitates conjugate updating of the concentration parameter in Gamma ratios, enabling full Bayesian inference for the aforementioned count distributions. We use DM models as our running examples. Our methodology leverages fast residue computation and admits closed-form posterior moments. Additionally, we recommend a default horseshoe type prior which has a heavy tail and substantial mass around zero. It admits continuous shrinkage, making the posterior highly adaptable to sparsity or quasi-sparsity in the data. Furthermore, we offer insights and potential generalizations to other count models facing the two challenges. We demonstrate the usefulness of our approach on both simulated examples and on real-world applications. Finally, we conclude with directions for future research.
翻译:暂无翻译