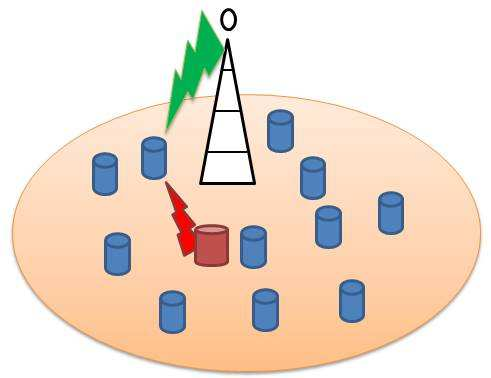
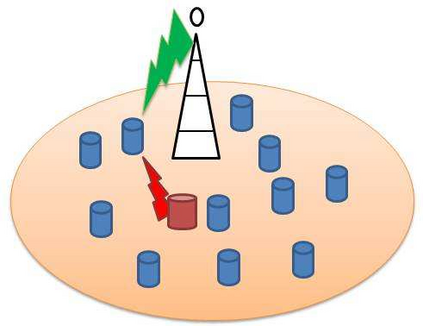
We consider a communication system where a base station (BS) transmits update packets to $N$ users, one user at a time, over a wireless channel. We investigate the age of this status updating system with an adversary that jams the update packets in the downlink. We consider two system models: with diversity and without diversity. In the model without diversity, we show that if the BS schedules the users with a stationary randomized policy, then the optimal choice for the adversary is to block the user which has the lowest probability of getting scheduled by the BS, at the middle of the time horizon, consecutively for $\alpha T$ time slots. In the model with diversity, we show that for large $T$, the uniform user scheduling algorithm together with the uniform sub-carrier choosing algorithm is $\frac{2 N_{sub}}{N_{sub}-1}$ optimal. Next, we investigate the game theoretic equilibrium points of this status updating system. For the model without diversity, we show that a Nash equilibrium does not exist, however, a Stackelberg equilibrium exists when the scheduling algorithm of the BS acts as the leader and the adversary acts as the follower. For the model with diversity, we show that a Nash equilibrium exists and identify the Nash equilibrium. Finally, we extend the model without diversity to the case where the BS can serve multiple users and the adversary can jam multiple users, at a time.
翻译:我们考虑一个通信系统,让一个基地站(BS)通过无线频道将更新包传送给一个用户,一个用户,一个用户,一个用户,一个用户,一个用户,一个无线频道。我们调查这个状态更新系统的老旧时间段的老旧时间段。我们用一个在下行连接更新包的对手来调查这个状态更新系统。我们考虑两个系统模式:多样性和没有多样性的系统模式。在没有多样性的模型中,如果BS安排用户使用固定随机化政策,那么对手的最佳选择是阻止一个用户在时间段中间最有可能被BS安排到一个美元-alpha T$时间段的用户。在有多样性的模型中,我们用大T美元来调查这个状态更新系统的时间段的老旧时间段的老旧时间段。我们显示,对于大T$T$,统一用户与统一的分包机选择的算法是$frac{2N<unk> 2 N<unk> susub<unk> N<unk> {sub}-1}最佳的。我们调查这个状态更新系统的游戏的平衡点。对于没有多样性的模型来说,但是,我们显示纳什平衡并不存在,当BS的模型的模型的模型的模型的模型的模型的多重用户作为最终的领袖,然后显示,我们可以展示的平衡。</s>