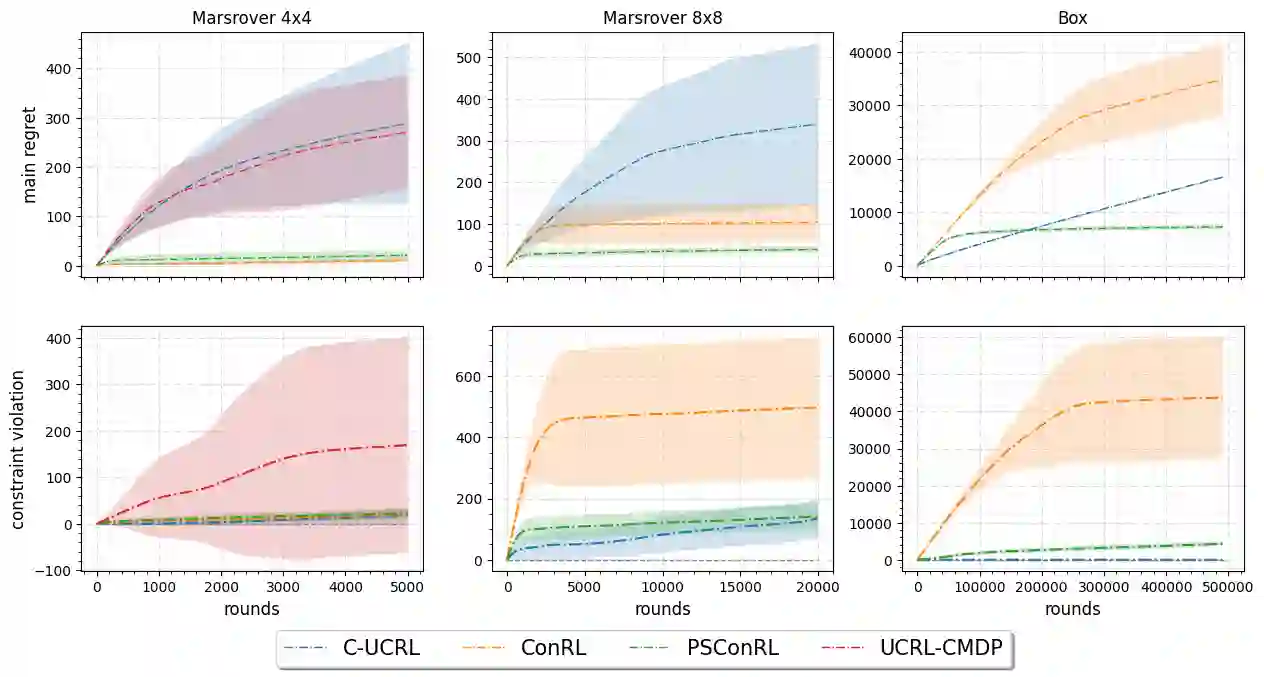
We present a new algorithm based on posterior sampling for learning in constrained Markov decision processes (CMDP) in the infinite-horizon undiscounted setting. The algorithm achieves near-optimal regret bounds while being advantageous empirically compared to the existing algorithms. Our main theoretical result is a Bayesian regret bound for each cost component of \tilde{O} (HS \sqrt{AT}) for any communicating CMDP with S states, A actions, and bound on the hitting time H. This regret bound matches the lower bound in order of time horizon T and is the best-known regret bound for communicating CMDPs in the infinite-horizon undiscounted setting. Empirical results show that, despite its simplicity, our posterior sampling algorithm outperforms the existing algorithms for constrained reinforcement learning.
翻译:暂无翻译