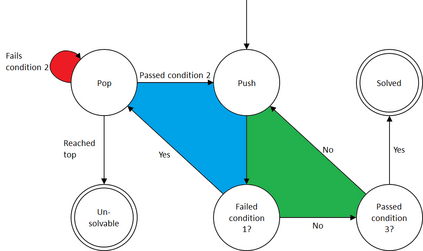
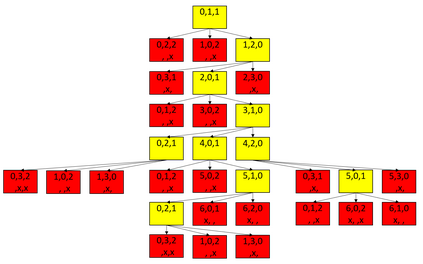
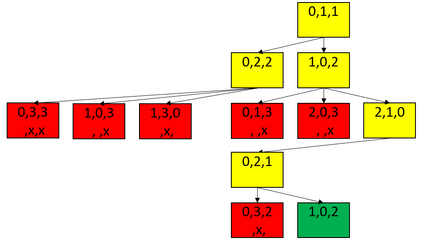
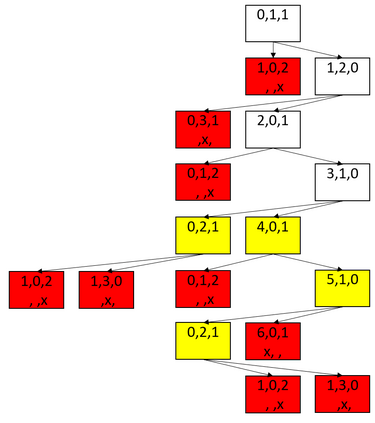
Pinwheel Scheduling aims to find a perpetual schedule for unit-length tasks on a single machine subject to given maximal time spans (a.k.a. frequencies) between any two consecutive executions of the same task. The density of a Pinwheel Scheduling instance is the sum of the inverses of these task frequencies; the 5/6-Conjecture (Chan and Chin, 1993) states that any Pinwheel Scheduling instance with density at most 5/6 is schedulable. We formalize the notion of Pareto surfaces for Pinwheel Scheduling and exploit novel structural insights to engineer an efficient algorithm for computing them. This allows us to (1) confirm the 5/6-Conjecture for all Pinwheel Scheduling instances with at most 12 tasks and (2) to prove that a given list of only 23 schedules solves all schedulable Pinwheel Scheduling instances with at most 5 tasks.
翻译:Pin轮式排队的目的是为同一任务连续执行两次任务之间的最大时间间隔(a.k.a.频率)为单一机器找到一个长期的单体长任务时间表。 Pin轮式排队实例的密度是这些任务频率的反数的总和;5/6-弹道(Chan和Chin,1993年)指出,密度最多为5/6的任何Pin轮式排队实例都是可排队的。我们正式确定了Pin轮式排队使用的Pareto表面概念,并利用新的结构洞察来设计一种高效的计算算法。这使我们能够(1) 确认所有轮式排队的5/6射线,最多有12个任务,(2) 证明一个只有23个计时表的列表能解决所有可排队的Pin轮式排队案例,最多有5个任务。