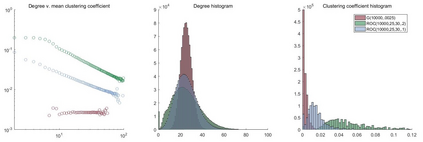
How can we approximate sparse graphs and sequences of sparse graphs (with unbounded average degree)? We consider convergence in the first $k$ moments of the graph spectrum (equivalent to the numbers of closed $k$-walks) appropriately normalized. We introduce a simple, easy to sample, random graph model that captures the limiting spectra of many sequences of interest, including the sequence of hypercube graphs. The Random Overlapping Communities (ROC) model is specified by a distribution on pairs $(s,q)$, $s \in \mathbb{Z}_+, q \in (0,1]$. A graph on $n$ vertices with average degree $d$ is generated by repeatedly picking pairs $(s,q)$ from the distribution, adding an Erd\H{o}s-R\'{e}nyi random graph of edge density $q$ on a subset of vertices chosen by including each vertex with probability $s/n$, and repeating this process so that the expected degree is $d$. Our proof of convergence to a ROC random graph is based on the Stieltjes moment condition. We also show that the model is an effective approximation for individual graphs. For almost all possible triangle-to-edge and four-cycle-to-edge ratios, there exists a pair $(s,q)$ such that the ROC model with this single community type produces graphs with both desired ratios, a property that cannot be achieved by stochastic block models of bounded description size. Moreover, ROC graphs exhibit an inverse relationship between degree and clustering coefficient, a characteristic of many real-world networks.
翻译:我们怎样可以粗略地估计稀少的图表和图表序列(没有约束的平均度)? 我们考虑在图形频谱最初的美元时段( 相当于关闭的美元行进数) 适当地正常化。 我们引入一个简单、 容易取样的随机图形模型, 捕捉许多利益序列的有限光谱, 包括超立方图的序列 。 随机重叠区( ROC) 模式由双对( s, q) 美元, $\ in\ mathbblock, q rbbc =( 0, 1美元)? 一个平均水平的以美元为单位的硬盘的硬盘组合。 我们反复从分布中选取双对美元( q) 美元, 随机图模型, 在选择的每组顶端密度为 $ qqq 。 我们的正方正数 的正数 与正数 的正数, 也无法在直方形 的正数 模式中 。