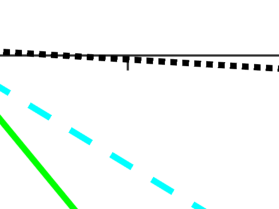
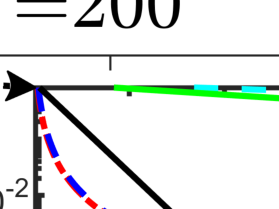
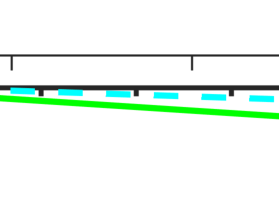
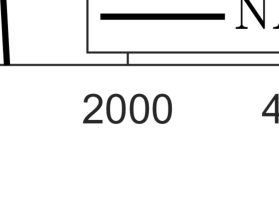
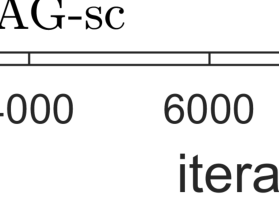
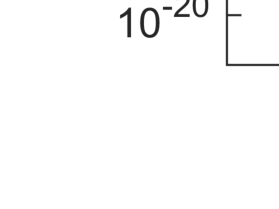The Nesterov accelerated gradient (NAG) method is an important extrapolation-based numerical algorithm that accelerates the convergence of the gradient descent method in convex optimization. When dealing with an objective function that is $\mu$-strongly convex, selecting extrapolation coefficients dependent on $\mu$ enables global R-linear convergence. In cases where $\mu$ is unknown, a commonly adopted approach is to set the extrapolation coefficient using the original NAG method. This choice allows for achieving the optimal iteration complexity among first-order methods for general convex problems. However, it remains unknown whether the NAG method with an unknown strongly convex parameter exhibits global R-linear convergence for strongly convex problems. In this work, we answer this question positively by establishing the Q-linear convergence of certain constructed Lyapunov sequences. Furthermore, we extend our result to the global R-linear convergence of the accelerated proximal gradient method, which is employed for solving strongly convex composite optimization problems. Interestingly, these results contradict the findings of the continuous counterpart of the NAG method in [Su, Boyd, and Cand\'es, J. Mach. Learn. Res., 2016, 17(153), 1-43], where the convergence rate by the suggested ordinary differential equation cannot exceed the $O(1/{\tt poly}(k))$ for strongly convex functions.
翻译:暂无翻译