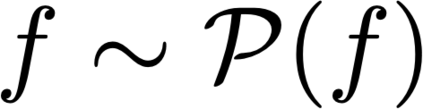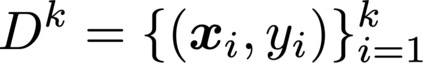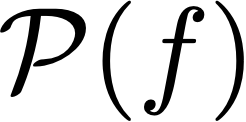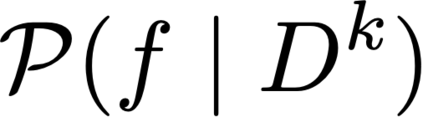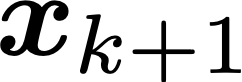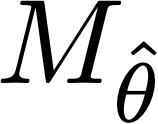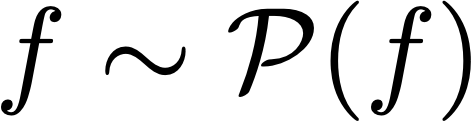This paper develops a finite-sample statistical theory for in-context learning (ICL), analyzed within a meta-learning framework that accommodates mixtures of diverse task types. We introduce a principled risk decomposition that separates the total ICL risk into two orthogonal components: Bayes Gap and Posterior Variance. The Bayes Gap quantifies how well the trained model approximates the Bayes-optimal in-context predictor. For a uniform-attention Transformer, we derive a non-asymptotic upper bound on this gap, which explicitly clarifies the dependence on the number of pretraining prompts and their context length. The Posterior Variance is a model-independent risk representing the intrinsic task uncertainty. Our key finding is that this term is determined solely by the difficulty of the true underlying task, while the uncertainty arising from the task mixture vanishes exponentially fast with only a few in-context examples. Together, these results provide a unified view of ICL: the Transformer selects the optimal meta-algorithm during pretraining and rapidly converges to the optimal algorithm for the true task at test time.
翻译:暂无翻译