Modelling matrix time series via a tensor CP-decomposition

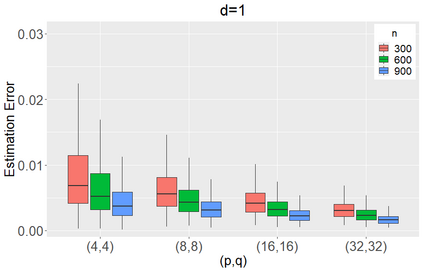
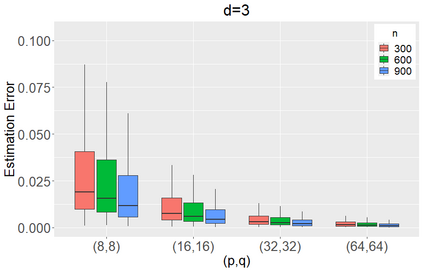
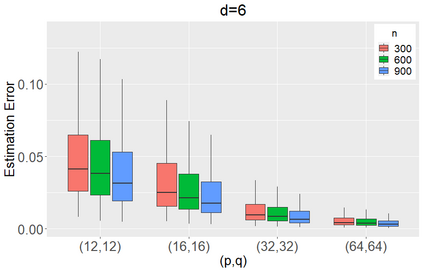
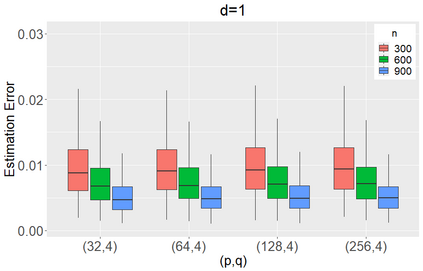
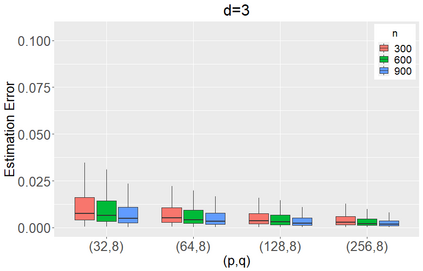
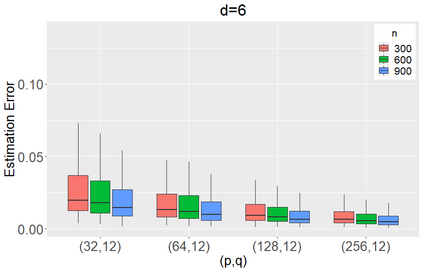
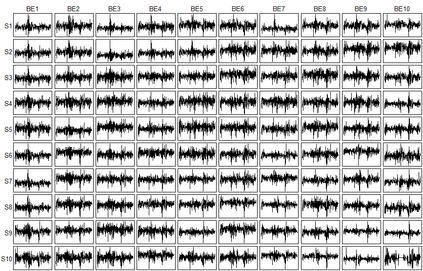
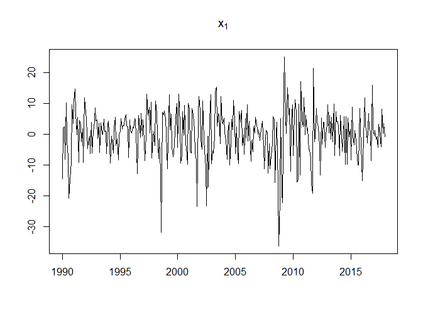
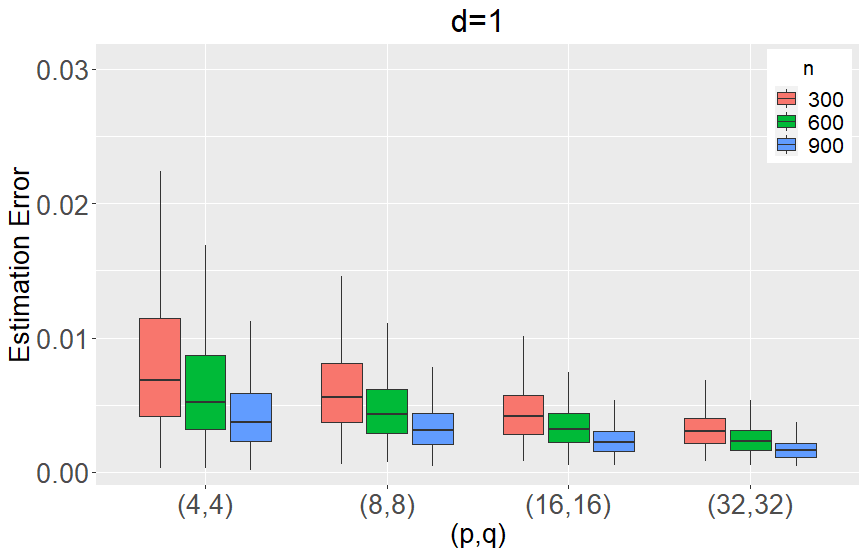
We propose to model matrix time series based on a tensor CP-decomposition. Instead of using an iterative algorithm which is the standard practice for estimating CP-decompositions, we propose a new and one-pass estimation procedure based on a generalized eigenanalysis constructed from the serial dependence structure of the underlying process. A key idea of the new procedure is to project a generalized eigenequation defined in terms of rank-reduced matrices to a lower-dimensional one with full-ranked matrices, to avoid the intricacy of the former of which the number of eigenvalues can be zero, finite and infinity. The asymptotic theory has been established under a general setting without the stationarity. It shows, for example, that all the component coefficient vectors in the CP-decomposition are estimated consistently with the different error rates, depending on the relative sizes between the dimensions of time series and the sample size. The proposed model and the estimation method are further illustrated with both simulated and real data; showing effective dimension-reduction in modelling and forecasting matrix time series.