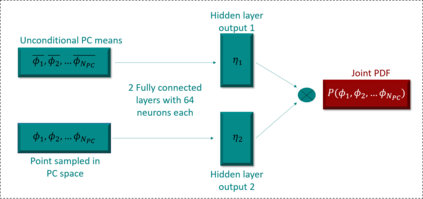
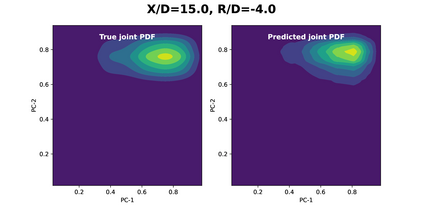
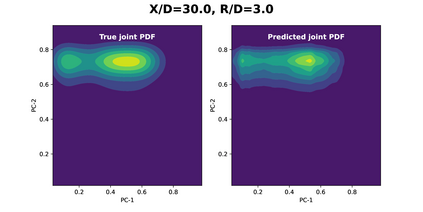
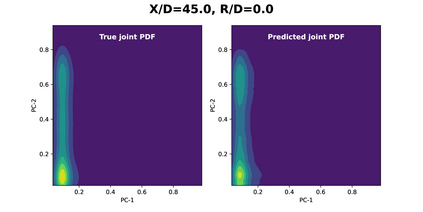
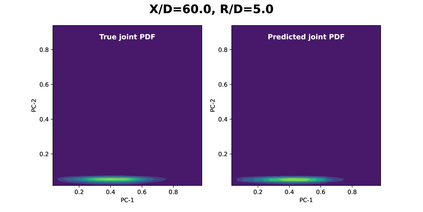
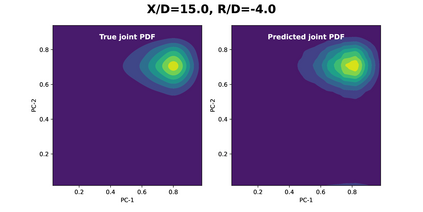
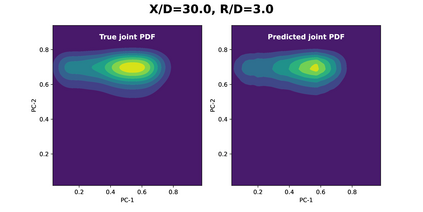
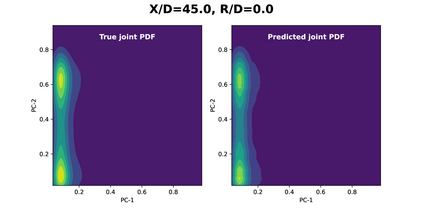
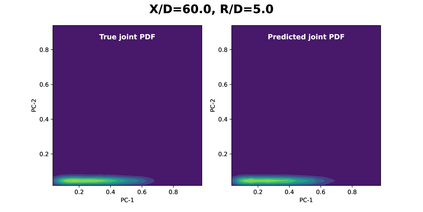
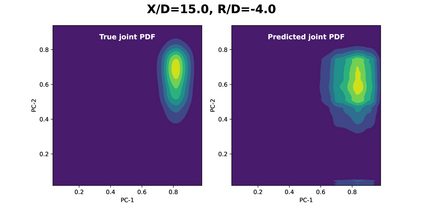
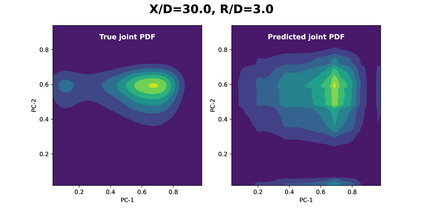
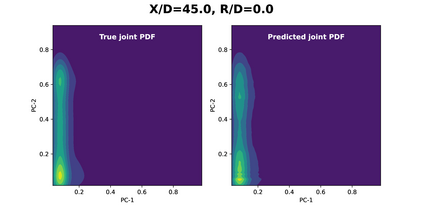
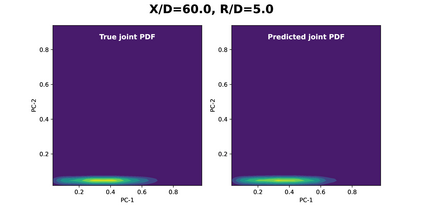
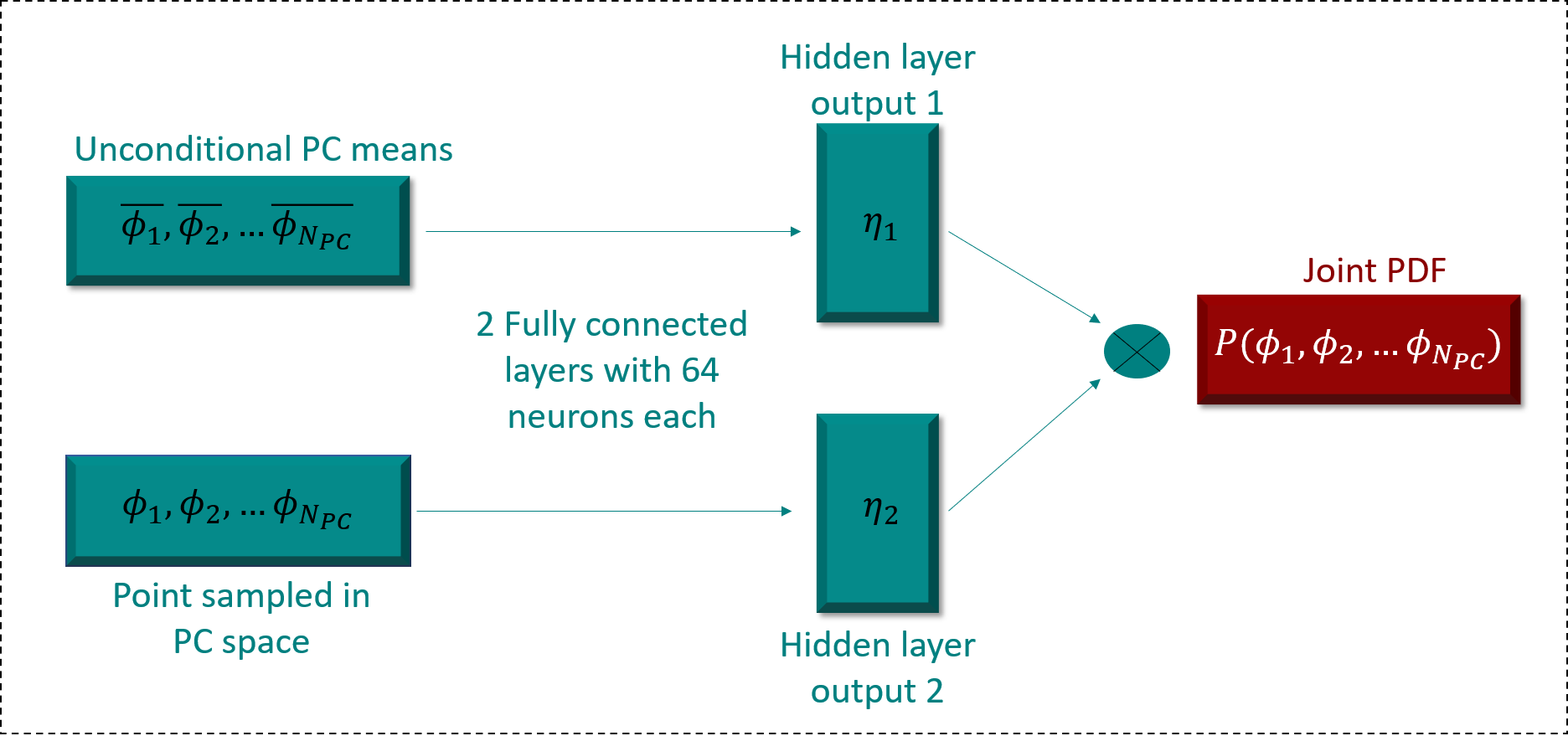
Joint probability density function (PDF)-based models in turbulent combustion provide direct closure for turbulence-chemistry interactions. The joint PDFs capture the turbulent flame dynamics at different spatial locations and hence it is crucial to represent them accurately. The jointPDFs are parameterized on the unconditional means of thermo-chemical state variables, which can be high dimensional. Thus, accurate construction of joint PDFs at various spatial locations may require an exorbitant amount of data. In a previous work, we introduced a framework that alleviated data requirements by constructing joint PDFs in a lower dimensional space using principal component analysis (PCA) in conjunction with Kernel Density Estimation (KDE). However, constructing the principal component (PC) joint PDFs is still computationally expensive as they are required to be calculated at each spatial location in the turbulent flame. In this work, we propose the concept of a generalized joint PDF model using the Deep Operator Network (DeepONet). The DeepONet is a machine learning model that is parameterized on the unconditional means of PCs at a given spatial location and discrete PC coordinates and predicts the joint probability density value for the corresponding PC coordinate. We demonstrate the accuracy and generalizability of the DeepONet on the Sandia flames, D, E and F. The DeepONet is trained based on the PC joint PDFs observed inflame E and yields excellent predictions of joint PDFs shapes at different spatial locations of flamesD and F, which are not seen during training
翻译:在动荡燃烧中,基于联合概率密度功能(PDF)的混合模型(PDF)为动荡化学相互作用提供了直接封闭。联合PDF为不同空间位置的动荡火焰动态提供了直接封闭。联合PDF为各个空间位置的动荡化学状态变量提供了参数。因此,在不同空间位置准确构建联合PDF可能需要大量数据。在先前的工作中,我们引入了一个框架,通过在低维空间使用主要组成部分分析(PCA)与内核密度估计(KDE)一起构建联合PDF,从而缓解数据需求。然而,建立主要组成部分(PC)联合PDFF仍然计算成本高昂,因为需要在动荡火焰中每个空间位置计算这些参数。因此,我们建议使用深操作网络(DeepONet)建立一个通用的联合PDFF模型概念概念。DeepONet是一个机器学习模型,在特定空间位置和离心的离心空间密度密度密度密度(PCAA)分析(PCA)中,而不是离心的PDFCFCM 坐标和直径的精确度(我们所训练的CFDFPDF) 的精确度测试的精确度中,我们根据共同的精确度来演示的精确度来显示。