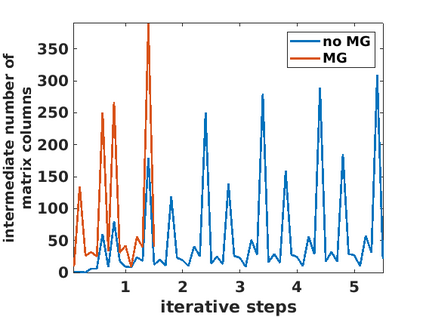
We introduce tensor numerical techniques for solving optimal control problems constrained by elliptic operators in $\mathbb{R}^d$, $d=2,3$, with variable coefficients, which can be represented in a low rank separable form. We construct a preconditioned iterative method with an adaptive rank truncation for solving the equation for the control function, governed by a sum of the elliptic operator and its inverse $M=A + A^{-1}$, both discretized over large $n^{\otimes d}$, $d=2,3$, spatial grids. Two basic solution schemes are proposed and analyzed. In the first approach, one solves iteratively the initial linear system of equations with the matrix $M$ such that the matrix vector multiplication with the elliptic operator inverse, $y=A^{-1} u,$ is performed as an embedded iteration by using a rank-structured solver for the equation of the form $A y=u$. The second numerical scheme avoids the embedded iteration by reducing the initial equation to an equivalent one with the polynomial system matrix of the form $A^2 +I$. For both schemes, a low Kronecker rank spectrally equivalent preconditioner is constructed by using the corresponding matrix valued function of the anisotropic Laplacian diagonalized in the Fourier basis. Numerical tests for control problems in 2D setting confirm the linear-quadratic complexity scaling of the proposed method in the univariate grid size $n$. Further, we numerically demonstrate that for our low rank solution method, a cascadic multigrid approach reduces the number of PCG iterations considerably, however the total CPU time remains merely the same as for the unigrid iteration.
翻译:我们引入了高压数字技术, 以解决由椭圆操作器以$mathbb{R ⁇ d$, $d=2, 3$, 以可变系数, 以低等级分解的形式表示。 我们构建了一种具有适应性级分解的迭接方法, 用于解析控制功能方程式的方程式, 由椭圆操作器及其逆值 $M=A+A+A ⁇ -1}来管理, 两者都分解为美元=美元, 美元=2, 3美元, 空间电网。 提出并分析了两种基本解决方案。 在第一个方法中, 一种是迭代解决初始线性方程式的线性系统, 以低级别分级分解为单位, 一种是基数的基数, 基数为基数的基数为基数的基数, 基数的基数乘基数乘基数的基数乘基数, 基数基数的基数的基数乘基数的基数乘基数为基数的基数, 基数的基数为基数的基数的基数的基数的基数为基数的基数的基数的基数, 基数的基数为基数的基数的基数的基数的基数的基数的基数, 基数的基数的基数的基数为基数的基数的基数的基数的基数的基数的基数的基数的基数的基数的基数, 。