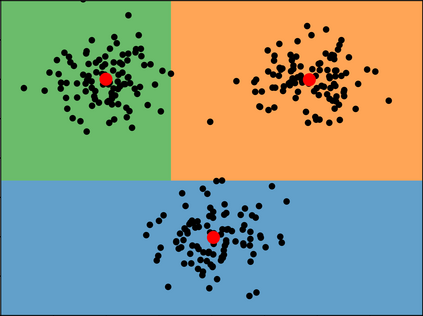
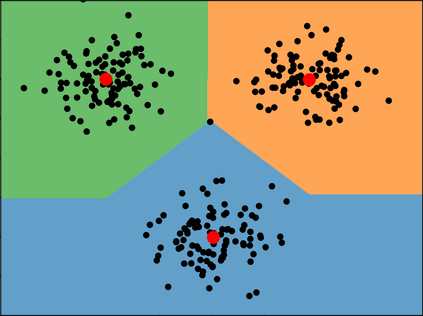
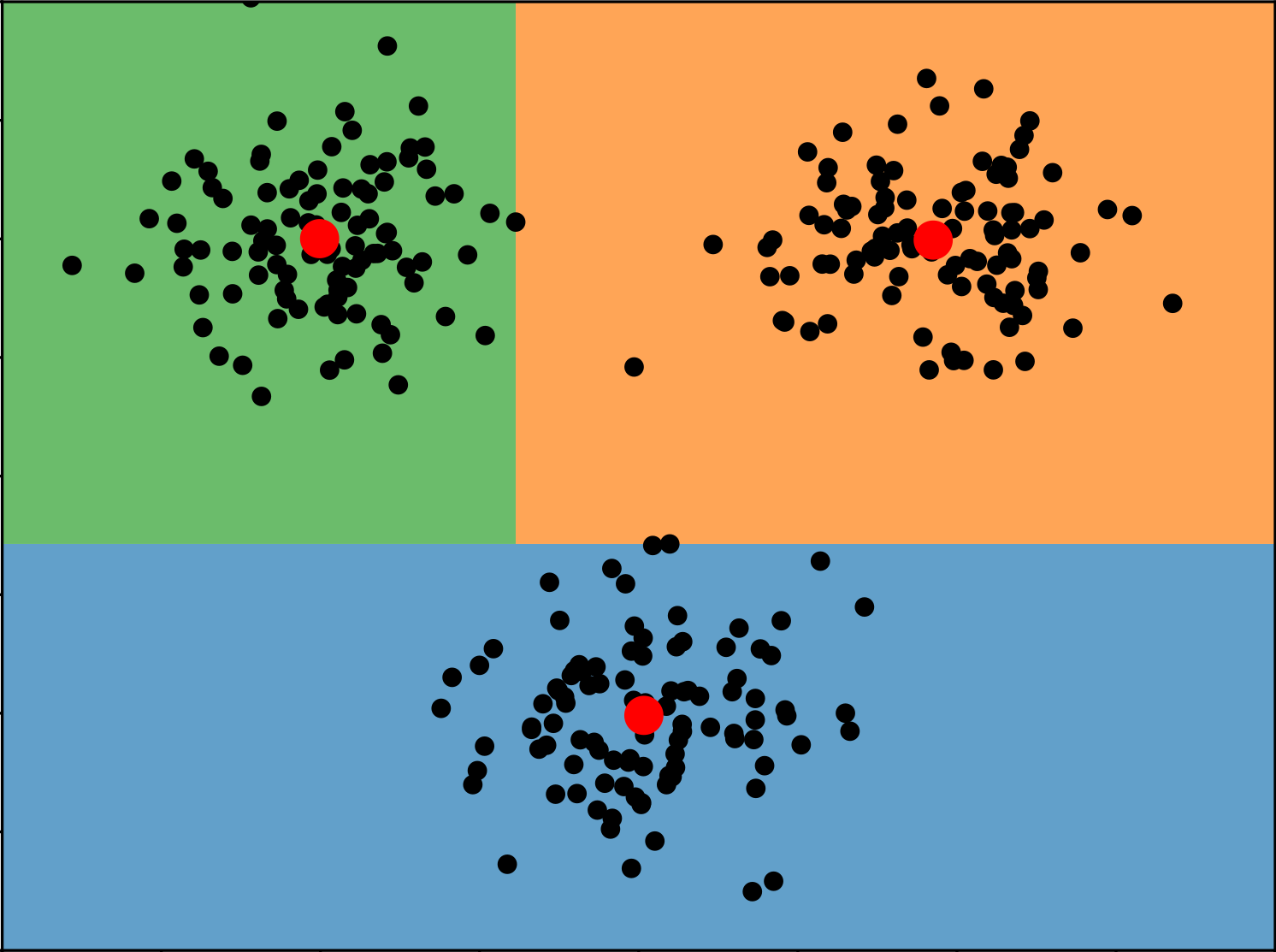
We show that the RandomCoordinateCut algorithm gives the optimal competitive ratio for explainable k-medians in l1. The problem of explainable k-medians was introduced by Dasgupta, Frost, Moshkovitz, and Rashtchian in 2020. Several groups of authors independently proposed a simple polynomial-time randomized algorithm for the problem and showed that this algorithm is O(log k loglog k) competitive. We provide a tight analysis of the algorithm and prove that its competitive ratio is upper bounded by 2ln k +2. This bound matches the Omega(log k) lower bound by Dasgupta et al (2020).
翻译:我们表明,在l1中随机坐标切割算法给出了可解释的k-中位数问题的最优竞争比。Dasgupta、Frost、Moshkovitz和Rashtchian于2020年引入了可解释的k-中位数问题。几组作者独立地为该问题提出了一种简单的多项式时间随机算法,并证明该算法是O(log k loglog k)竞争的。我们对该算法进行了紧密的分析,并证明其竞争比上限为2ln k +2。该界限匹配了Dasgupta等人(2020)的Ω(log k)下界。