Score Matching for Truncated Density Estimation on a Manifold

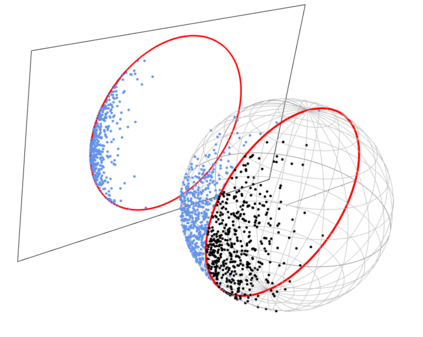
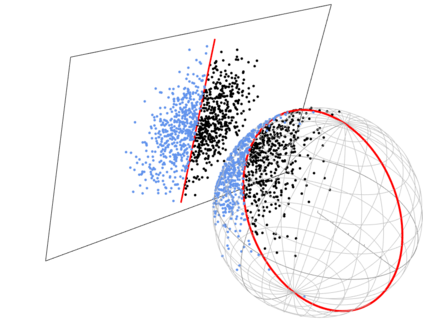
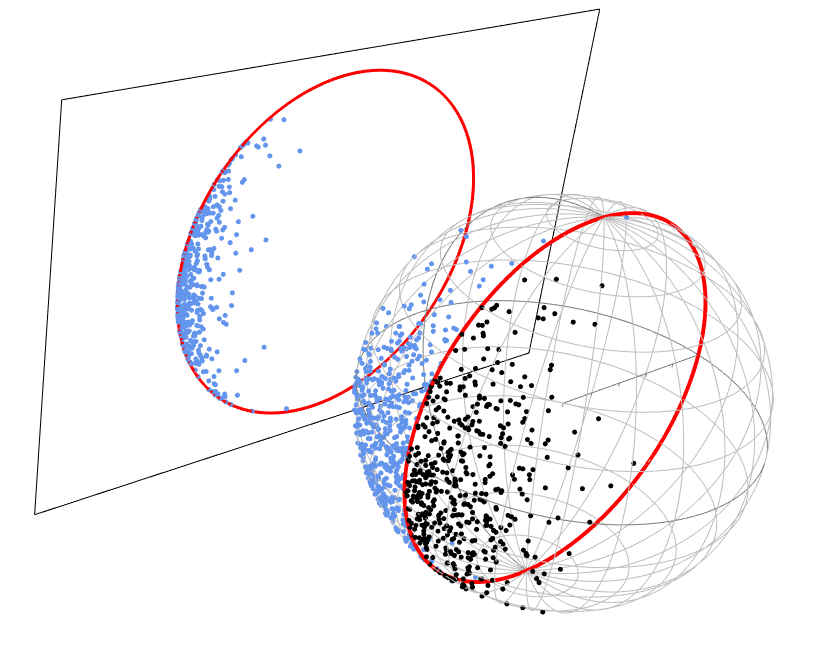
When observations are truncated, we are limited to an incomplete picture of our dataset. Recent methods deal with truncated density estimation problems by turning to score matching, where the access to the intractable normalising constant is not required. We present a novel extension to truncated score matching for a Riemannian manifold. Applications are presented for the von Mises-Fisher and Kent distributions on a two dimensional sphere in $\R^3$, as well as a real-world application of extreme storm observations in the USA. In simulated data experiments, our score matching estimator is able to approximate the true parameter values with a low estimation error and shows improvements over a maximum likelihood estimator.