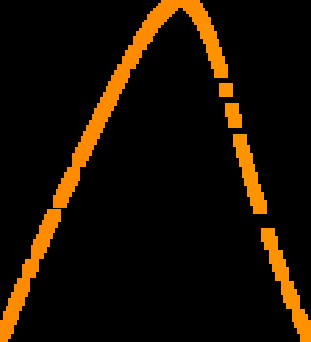
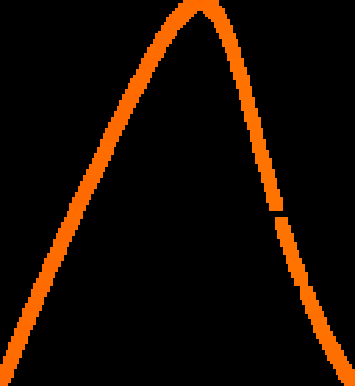
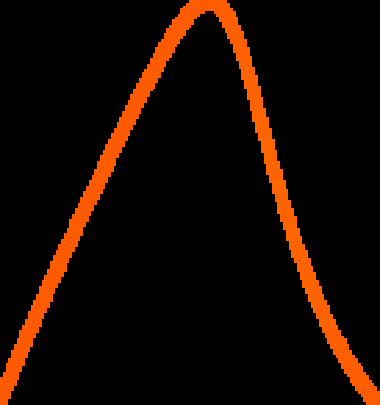
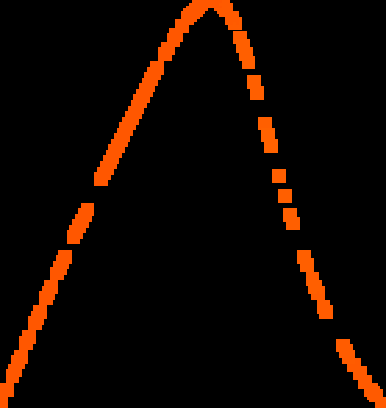
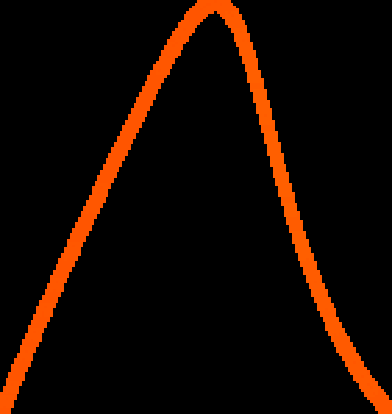
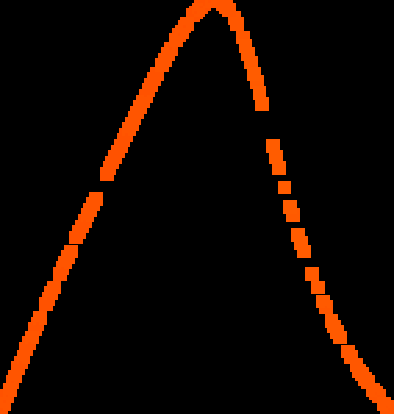
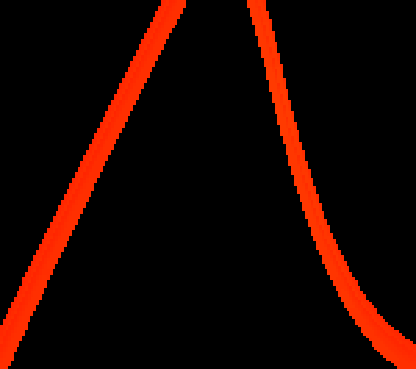
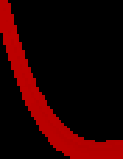
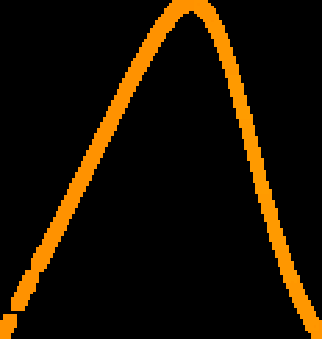
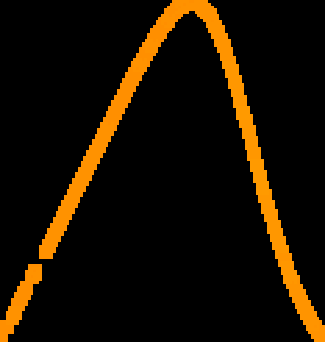
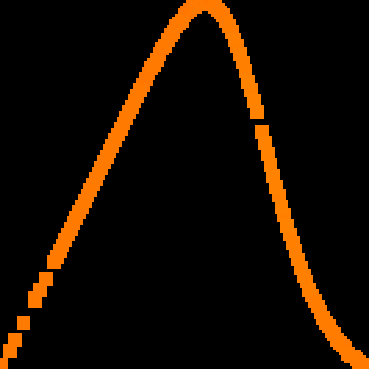
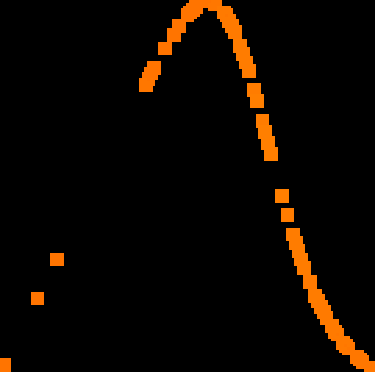
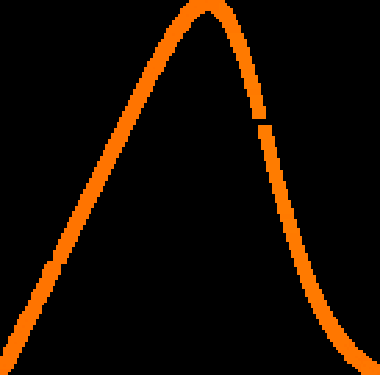
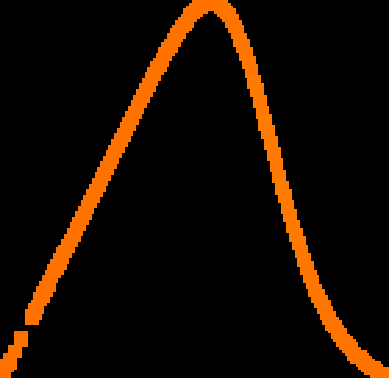
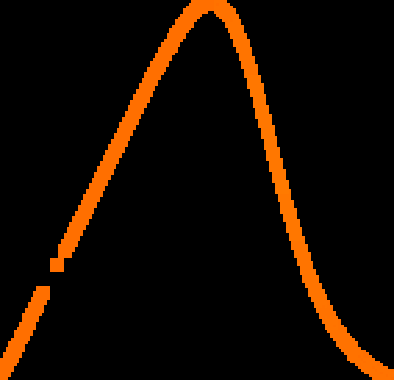
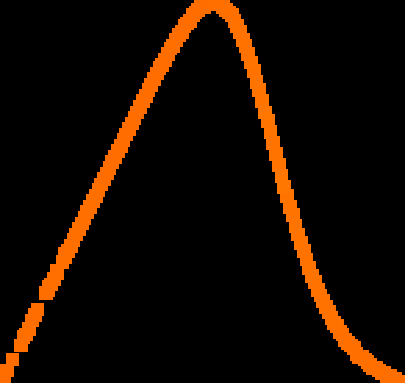
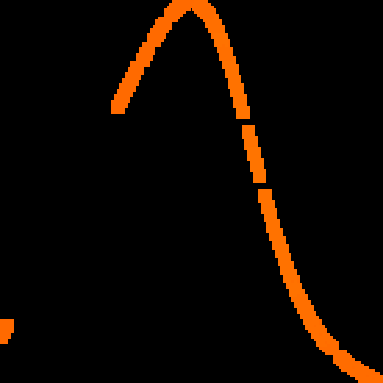
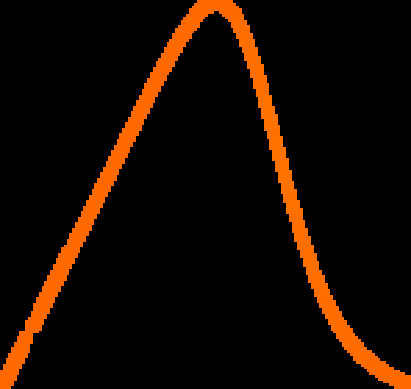
A novel way of using neural networks to learn the dynamics of time delay systems from sequential data is proposed. A neural network with trainable delays is used to approximate the right hand side of a delay differential equation. We relate the delay differential equation to an ordinary differential equation by discretizing the time history and train the corresponding neural ordinary differential equation (NODE) to learn the dynamics. An example on learning the dynamics of the Mackey-Glass equation using data from chaotic behavior is given. After learning both the nonlinearity and the time delay, we demonstrate that the bifurcation diagram of the neural network matches that of the original system.
翻译:提出了一个利用神经网络从相继数据中学习时间延迟系统的动态的新方式。 使用可训练的延迟的神经网络来近似延迟差分方程式的右侧。 我们把延迟差分方程与普通差分方程联系起来, 将时间历史分开, 并训练相应的神经普通差分方程来学习动态。 给出了一个使用混乱行为数据学习麦基- 格拉斯方程动态的例子。 在了解非线性和时间延迟之后, 我们证明神经网络的双曲线图与原始系统相匹配 。