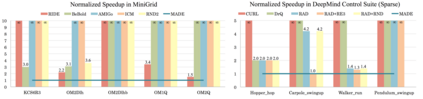
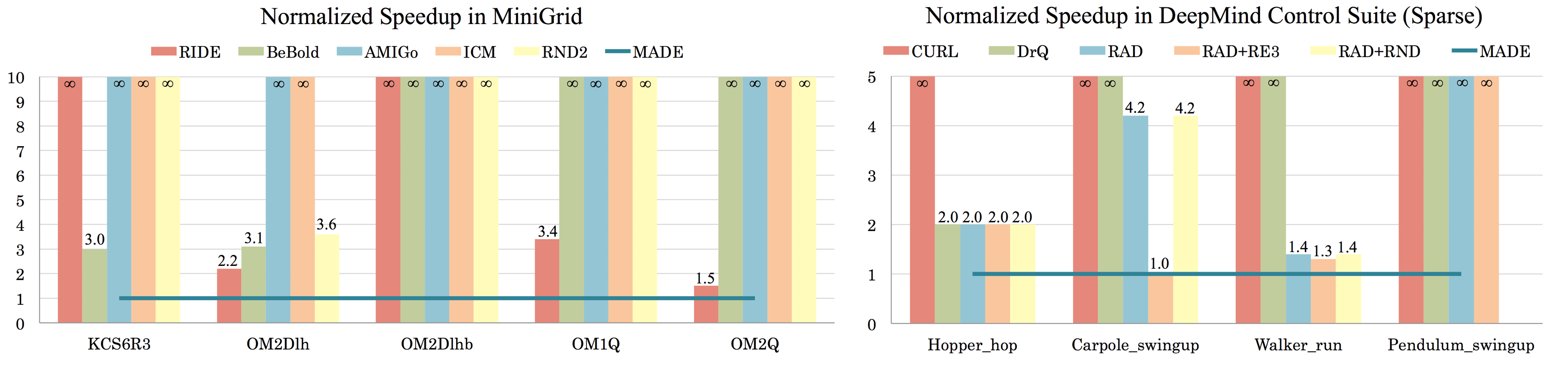
In online reinforcement learning (RL), efficient exploration remains particularly challenging in high-dimensional environments with sparse rewards. In low-dimensional environments, where tabular parameterization is possible, count-based upper confidence bound (UCB) exploration methods achieve minimax near-optimal rates. However, it remains unclear how to efficiently implement UCB in realistic RL tasks that involve non-linear function approximation. To address this, we propose a new exploration approach via \textit{maximizing} the deviation of the occupancy of the next policy from the explored regions. We add this term as an adaptive regularizer to the standard RL objective to balance exploration vs. exploitation. We pair the new objective with a provably convergent algorithm, giving rise to a new intrinsic reward that adjusts existing bonuses. The proposed intrinsic reward is easy to implement and combine with other existing RL algorithms to conduct exploration. As a proof of concept, we evaluate the new intrinsic reward on tabular examples across a variety of model-based and model-free algorithms, showing improvements over count-only exploration strategies. When tested on navigation and locomotion tasks from MiniGrid and DeepMind Control Suite benchmarks, our approach significantly improves sample efficiency over state-of-the-art methods. Our code is available at https://github.com/tianjunz/MADE.
翻译:在在线强化学习(RL)中,高效的探索在高维环境中仍然特别具有挑战性,且回报微弱。在低维环境中,有可能采用表格参数化,基于计数的上层信任(UCB)勘探方法可以达到最优化的最小质量。然而,如何在现实现实的RL任务中高效地执行UCB, 涉及非线性功能近似值。为了解决这个问题,我们建议采用一种新的探索方法,通过\ textit{mxxximizing} 来证明下一个政策与所探索区域不同。我们在标准RL目标中添加了这一术语,作为适应性的常规化调节器,以平衡勘探与开发之间的平衡。我们在将新目标配对成一种可察觉的趋同式算法,从而产生一种新的内在奖励,从而调整现有的奖金。提议的内在奖励很容易执行并与现有的其他RL算法相结合进行探索。作为概念的证明,我们评估各种基于模型和无模式的算法的列表范例的新内在奖赏,显示对仅计数的勘探战略的改进。我们在MiniGrid/DGMrMrgMrgnal控制方法上大大改进了我们的现有标准。