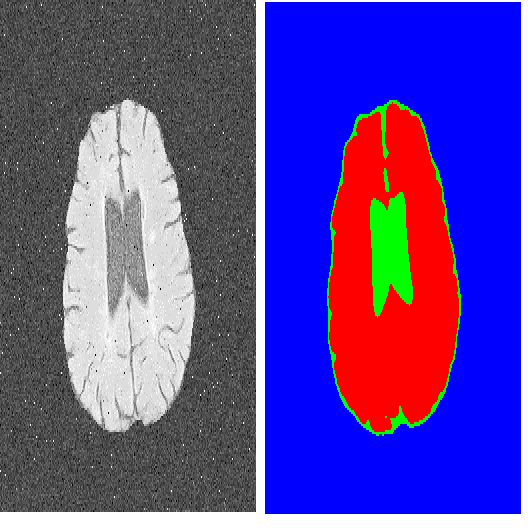
For image segmentation, the current standard is to perform pixel-level optimization and inference in Euclidean output embedding spaces through linear hyperplanes. In this work, we show that hyperbolic manifolds provide a valuable alternative for image segmentation and propose a tractable formulation of hierarchical pixel-level classification in hyperbolic space. Hyperbolic Image Segmentation opens up new possibilities and practical benefits for segmentation, such as uncertainty estimation and boundary information for free, zero-label generalization, and increased performance in low-dimensional output embeddings.
翻译:对于图像分解,当前标准是通过线性超天平在 Euclidea 输出嵌入空间中进行像素级优化和推断。 在这项工作中,我们显示双曲形元件为图像分解提供了宝贵的替代方法,并提出了双曲空间等级像素级分类的可移植配方。 双曲形图像分解为分解提供了新的可能性和实际效益,例如不确定性估算和边界信息,用于自由、零标签一般化和低维输出嵌入中性能增强。