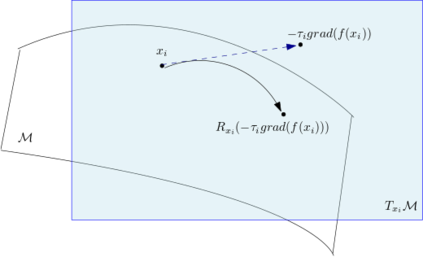
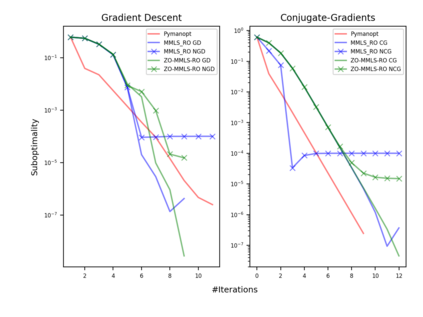
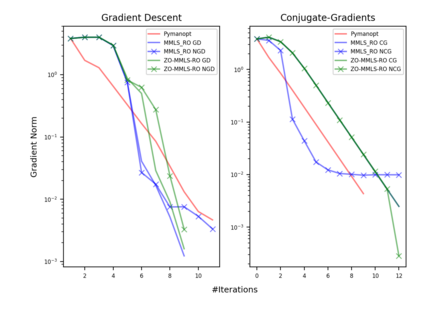
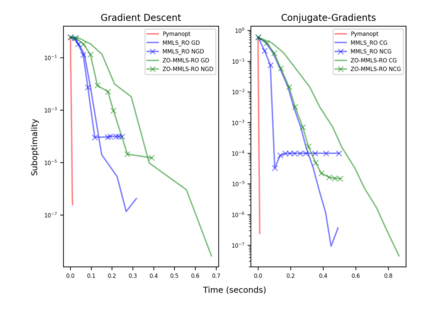
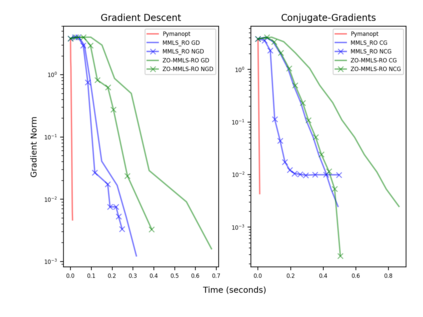
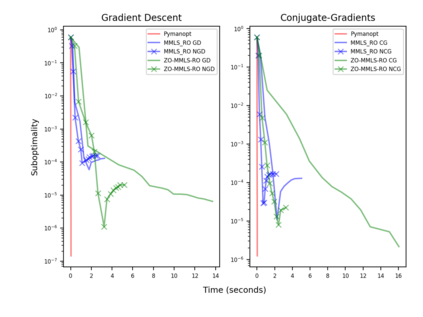
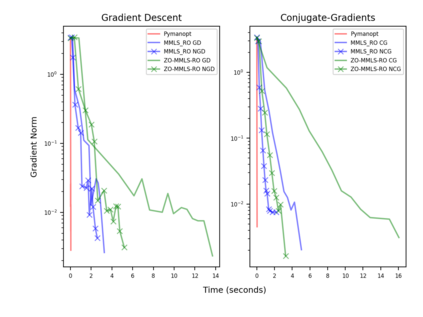
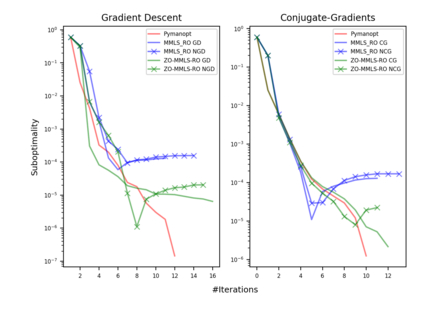
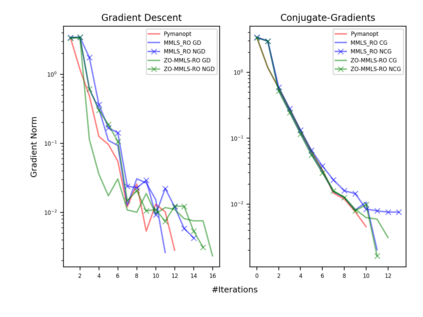
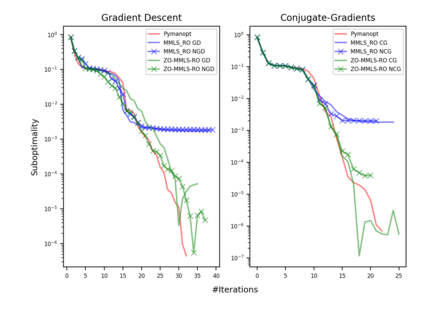
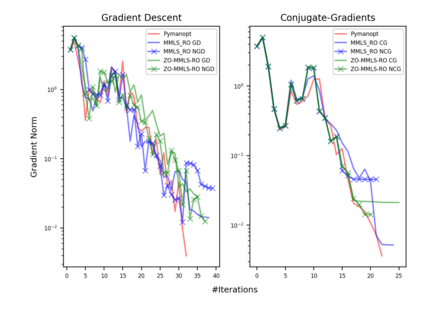
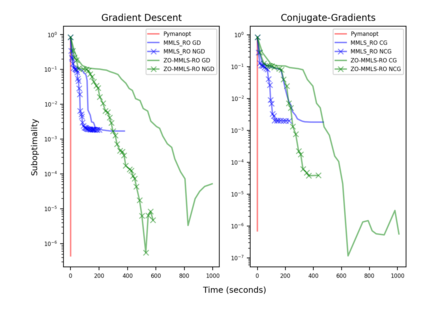
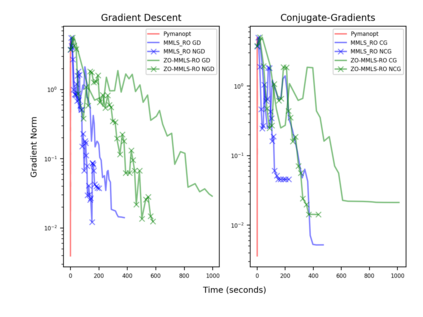
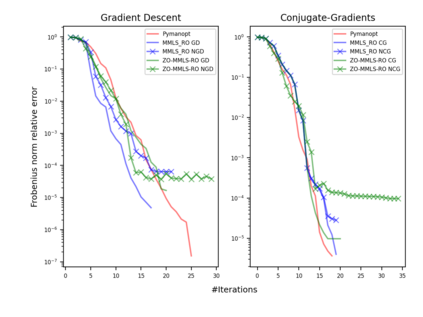
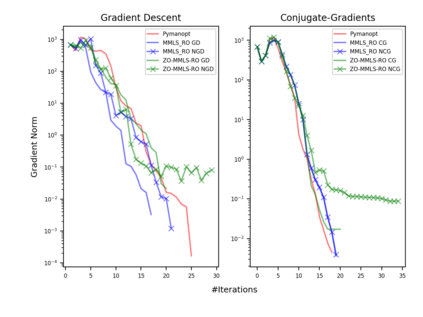
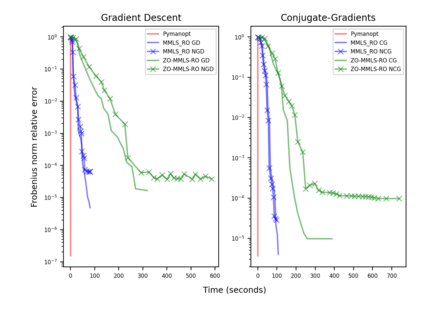
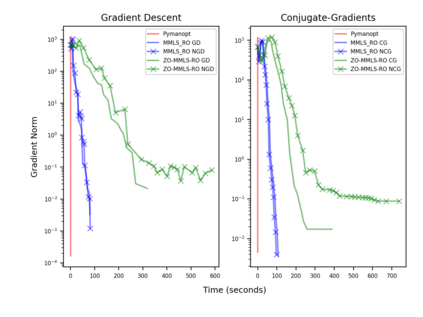
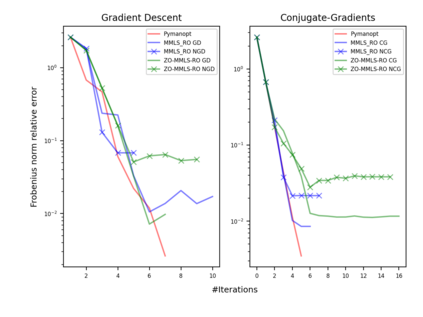
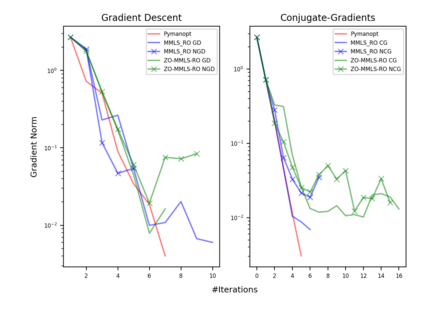
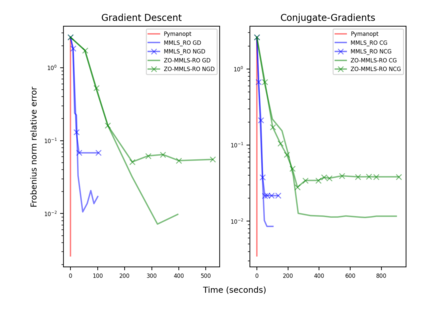
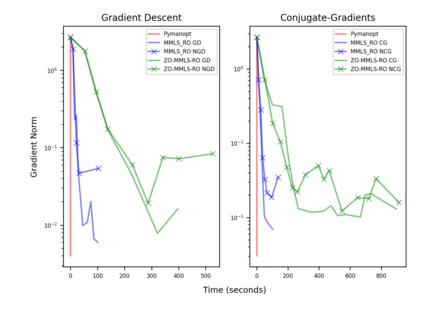
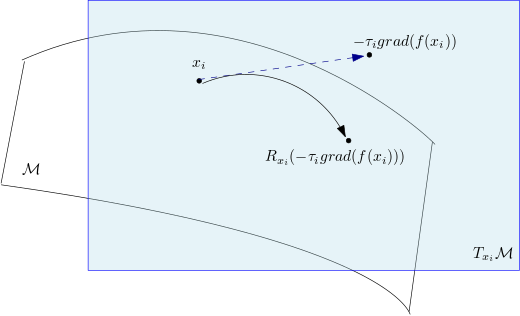
Riemannian optimization is a principled framework for solving optimization problems where the desired optimum is constrained to a smooth manifold $\mathcal{M}$. Algorithms designed in this framework usually require some geometrical description of the manifold, which typically includes tangent spaces, retractions, and gradients of the cost function. However, in many cases, only a subset (or none at all) of these elements can be accessed due to lack of information or intractability. In this paper, we propose a novel approach that can perform approximate Riemannian optimization in such cases, where the constraining manifold is a submanifold of $\R^{D}$. At the bare minimum, our method requires only a noiseless sample set of the cost function $(\x_{i}, y_{i})\in {\mathcal{M}} \times \mathbb{R}$ and the intrinsic dimension of the manifold $\mathcal{M}$. Using the samples, and utilizing the Manifold-MLS framework (Sober and Levin 2020), we construct approximations of the missing components entertaining provable guarantees and analyze their computational costs. In case some of the components are given analytically (e.g., if the cost function and its gradient are given explicitly, or if the tangent spaces can be computed), the algorithm can be easily adapted to use the accurate expressions instead of the approximations. We analyze the global convergence of Riemannian gradient-based methods using our approach, and we demonstrate empirically the strength of this method, together with a conjugate-gradients type method based upon similar principles.
翻译:riemannian 优化是一个解决优化问题的原则框架。 当理想的最佳化限制在平滑的 $$\ mathcal{M} $ 时, 优化是解决优化问题的一个原则框架。 在此框架中设计的量化标准通常需要一些对元数的几何描述, 通常包括成本函数的正切空格、 撤回和梯度。 但是, 在许多情况下, 由于缺乏信息或可吸引性, 这些元素中只有子集( 或完全没有) 可以访问。 本文中, 我们提出一种新的方法, 在这样的情形下, 最接近里曼的优化, 约束元值是 $\ R ⁇ D} 。 在最起码的时候, 我们的方法只需要对成本函数 $ (\ x ⁇ i}, y ⁇ } ) 和 渐变渐变的梯度进行无噪音的抽样描述。 但是, 如果使用某种精确的计算方法, 我们的计算方法, 也可以使用某种精确的计算方法 。