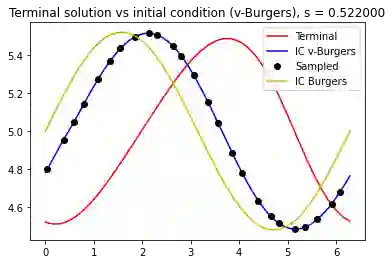
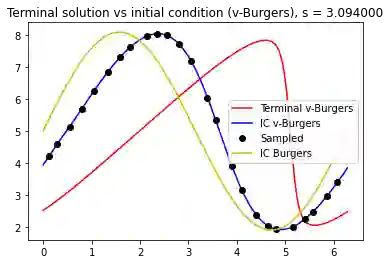
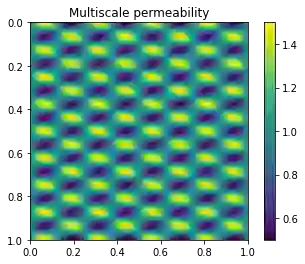
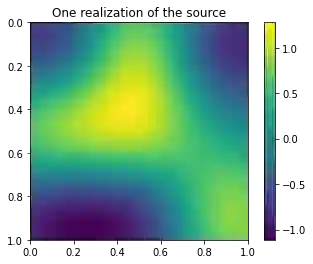
Operator learning trains a neural network to map functions to functions. An ideal operator learning framework should be mesh-free in the sense that the training does not require a particular choice of discretization for the input functions, allows for the input and output functions to be on different domains, and is able to have different grids between samples. We propose a mesh-free neural operator for solving parametric partial differential equations. The basis enhanced learning network (BelNet) projects the input function into a latent space and reconstructs the output functions. In particular, we construct part of the network to learn the ``basis'' functions in the training process. This generalized the networks proposed in Chen and Chen's universal approximation theory for the nonlinear operators to account for differences in input and output meshes. Through several challenging high-contrast and multiscale problems, we show that our approach outperforms other operator learning methods for these tasks and allows for more freedom in the sampling and/or discretization process.
翻译:操作员学习神经网络, 以绘制功能。 理想的操作员学习框架应该是无网格的, 也就是说, 培训不需要对输入功能进行特定的分解选择, 使输入和输出功能能够在不同领域存在, 并且能够有不同样本之间的网格。 我们建议用一个无网格的神经操作员来解决参数偏差方程式。 基础强化学习网络( BelNet) 将输入功能投向潜伏空间, 并重建输出功能。 特别是, 我们构建网络的一部分以学习培训过程中的“ basis” 功能。 这将陈氏和陈氏的通用近似理论中提议的网络推广到非线性操作员中, 以说明输入和输出中的差异。 我们通过几个挑战性的高调和多尺度问题, 显示我们的方法优于其他操作员学习这些任务的方法, 并允许在取样和/ 或分解过程中有更多的自由 。