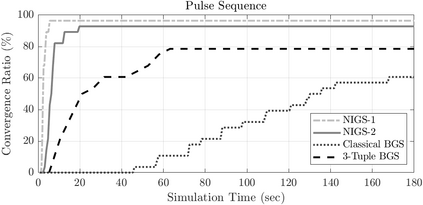
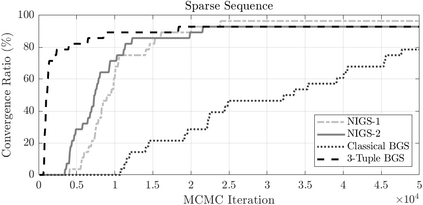
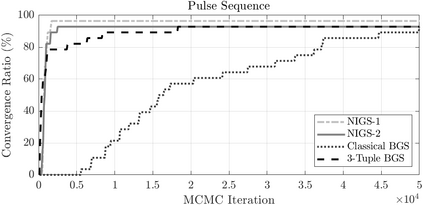
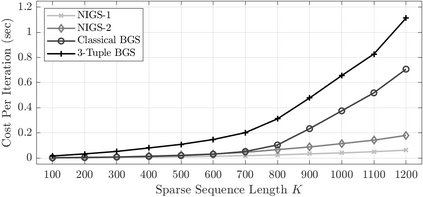
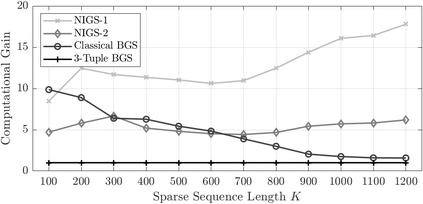
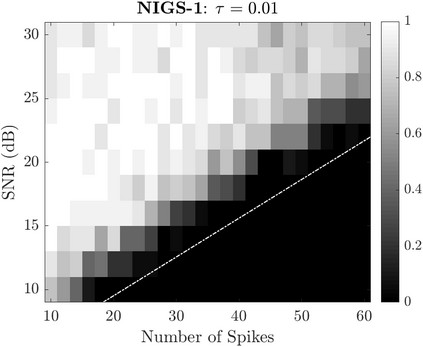
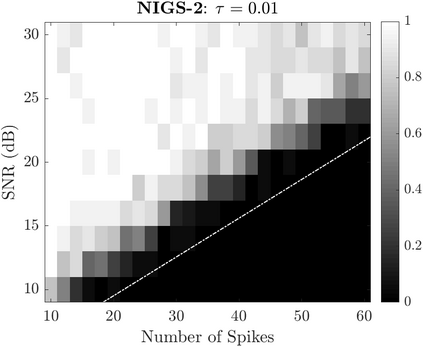
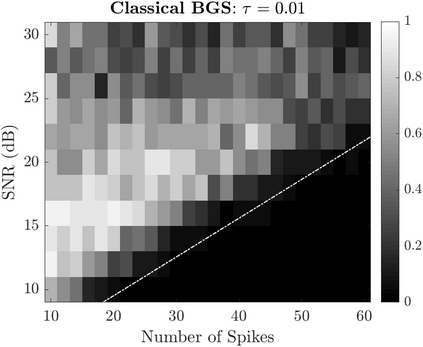
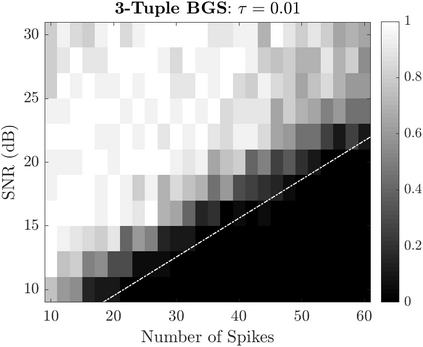
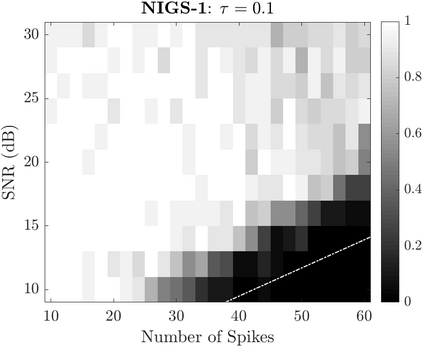
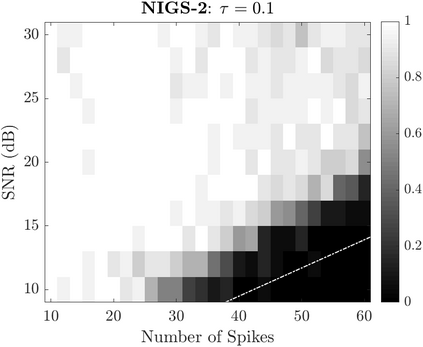
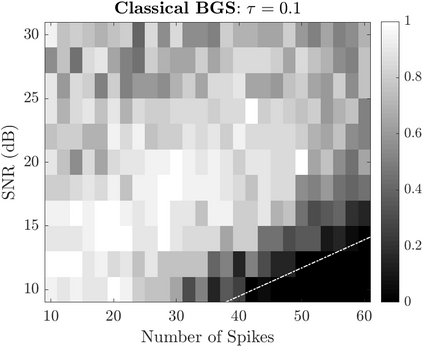
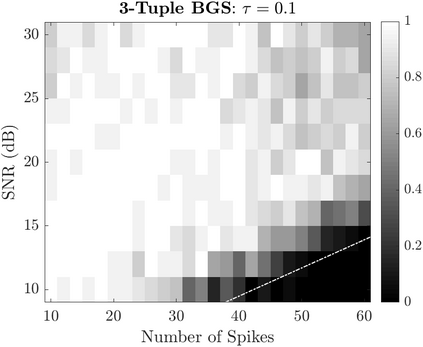
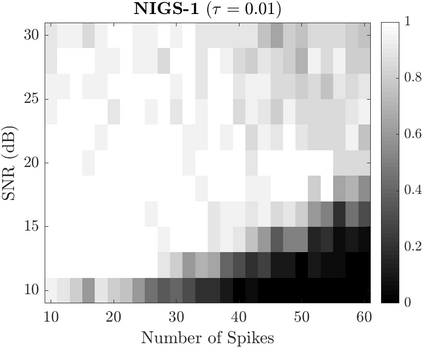
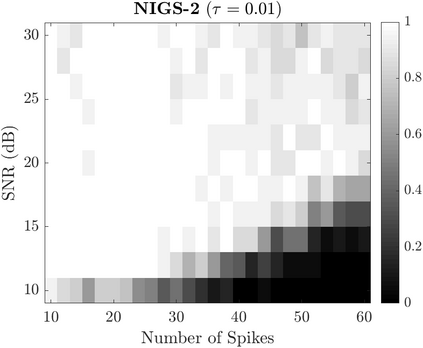
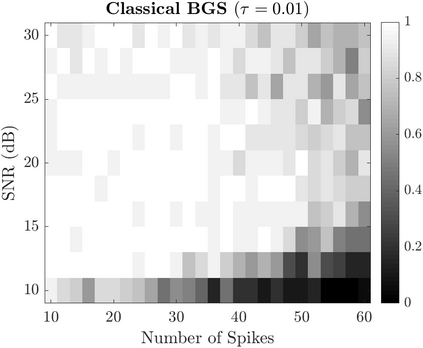
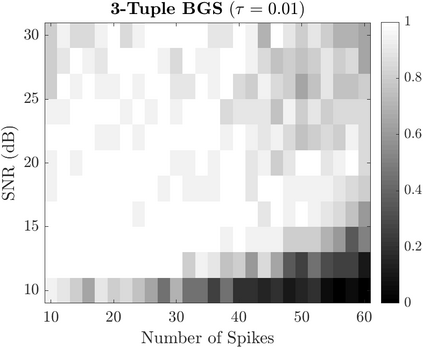
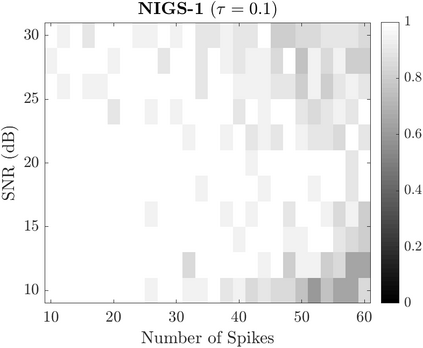
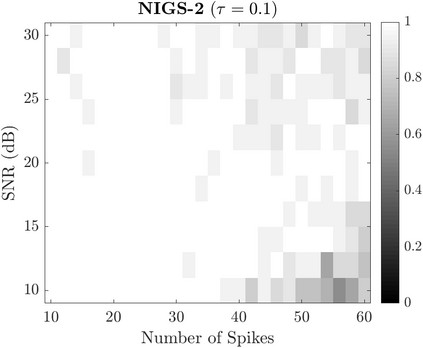
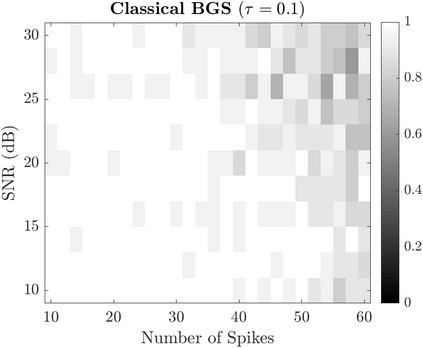
Bayesian estimation methods for sparse blind deconvolution problems conventionally employ Bernoulli-Gaussian (BG) prior for modeling sparse sequences and utilize Markov Chain Monte Carlo (MCMC) methods for the estimation of unknowns. However, the discrete nature of the BG model creates computational bottlenecks, preventing efficient exploration of the probability space even with the recently proposed enhanced sampler schemes. To address this issue, we propose an alternative MCMC method by modeling the sparse sequences using the Normal-Inverse-Gamma (NIG) prior. We derive effective Gibbs samplers for this prior and illustrate that the computational burden associated with the BG model can be eliminated by transferring the problem into a completely continuous-valued framework. In addition to sparsity, we also incorporate time and frequency domain constraints on the convolving sequences. We demonstrate the effectiveness of the proposed methods via extensive simulations and characterize computational gains relative to the existing methods that utilize BG modeling.
翻译:对稀有的盲目分解问题,Benesian估计方法通常使用Bernoulli-Gauussian(BG)来模拟稀有序列,并利用Markov链条Monte Carlo(MCMC)的方法来估计未知数,但是,BG模型的离散性质造成了计算瓶颈,即使最近提议的强化采样计划也妨碍了对概率空间的有效探索。为了解决这一问题,我们提议了另一种MCMCM方法,方法是利用普通反伽马(NIG)来模拟稀少序列。我们为之前的这一方法收集有效的Gibs采样器,并表明通过将问题转移到一个完全持续估价的框架,可以消除与BG模型相关的计算负担。除了简单易变之外,我们还将时间和频域限制纳入相关序列中。我们通过广泛的模拟来证明拟议方法的有效性,并描述与使用BG模型的现有方法相比的计算收益。