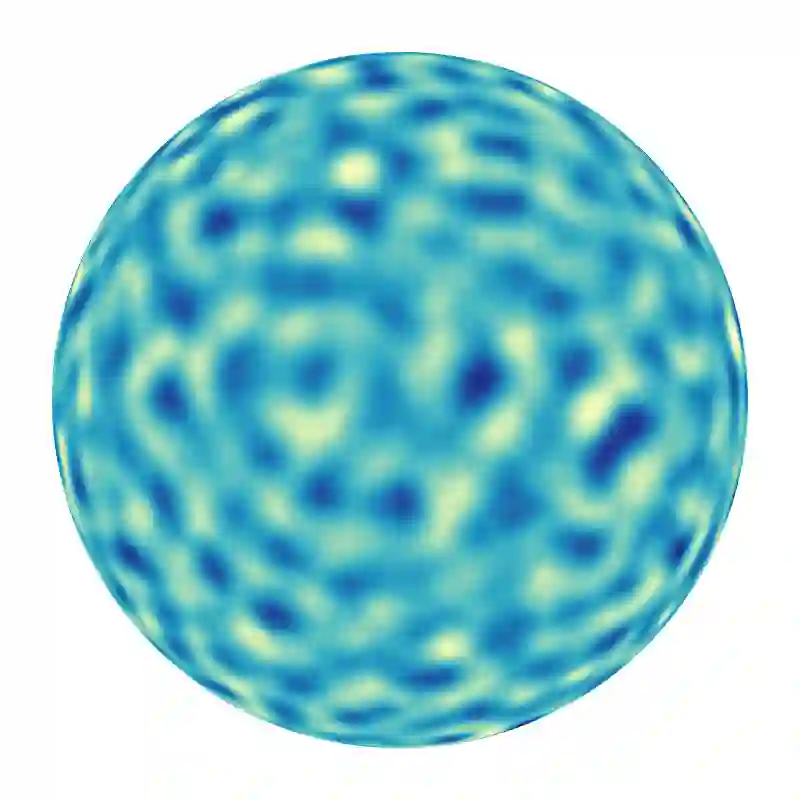
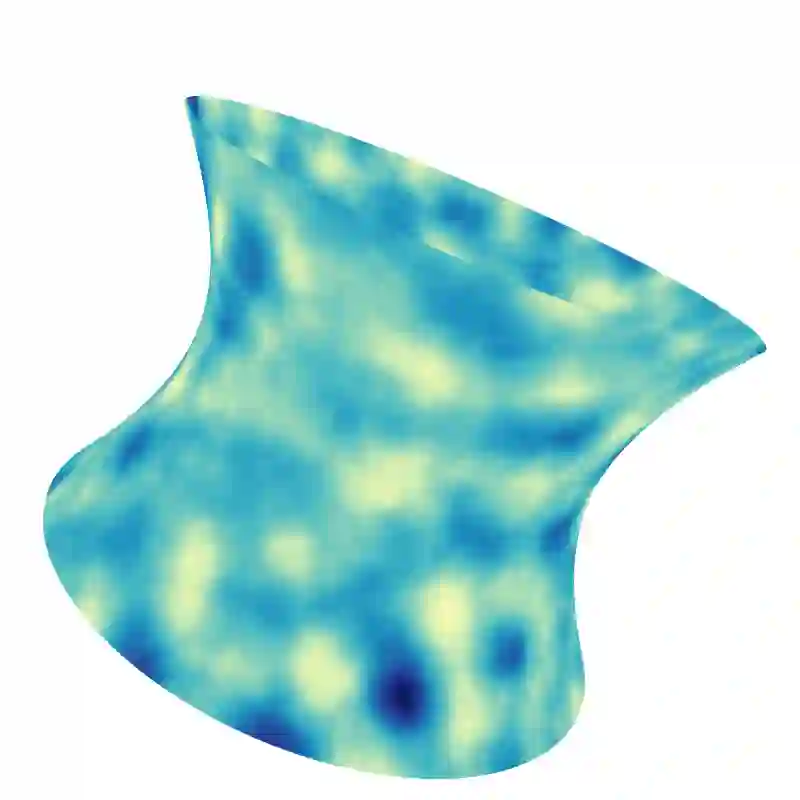
A new numerical approximation method for a class of Gaussian random fields on compact Riemannian manifolds is introduced. This class of random fields is characterized by the Laplace--Beltrami operator on the manifold. A Galerkin approximation is combined with a polynomial approximation using Chebyshev series. This so-called Galerkin--Chebyshev approximation scheme yields efficient and generic sampling algorithms for Gaussian random fields on manifolds. Strong and weak orders of convergence for the Galerkin approximation and strong convergence orders for the Galerkin--Chebyshev approximation are shown and confirmed through numerical experiments.
翻译:在紧凑的列伊曼尼方块上,为一类高斯随机字段采用了一种新的数字近似法。这种随机字段的特征是多管线上的Laplace-Beltrami操作员。Galerkin近似法与使用Chebyshev系列的多元近似法相结合。这种所谓的Galerkin-Chebyshev近似法为高斯随机字段的多管线提供了高效和通用的抽样算法。Galerkin近似法和加列尔金-切比谢夫近似法的强烈趋同令的强大和薄弱的趋同顺序通过数字实验得到显示和确认。