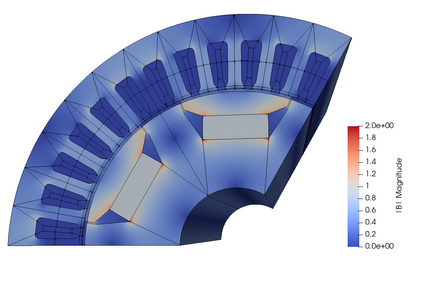
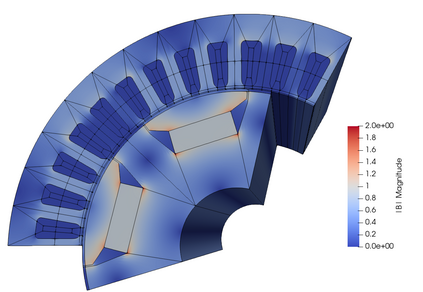
When applying isogeometric analysis to engineering problems, one often deals with multi-patch spline spaces that have incompatible discretisations, e.g. in the case of moving objects. In such cases mortaring has been shown to be advantageous. This contribution discusses the appropriate B-spline spaces needed for the solution of Maxwell's equations in the functions space H(curl) and the corresponding mortar spaces. The main contribution of this paper is to show that in formulations requiring gauging, as in the vector potential formulation of magnetostatic equations, one can remove the discrete kernel subspace from the mortared spaces by the graph-theoretical concept of a tree-cotree decomposition. The tree-cotree decomposition is done based on the control mesh, it works for non-contractible domains, and it can be straightforwardly applied independently of the degree of the B-spline bases. Finally, the simulation workflow is demonstrated using a realistic model of a rotating permanent magnet synchronous machine.
翻译:当对工程问题应用等离子分析时,人们往往会处理具有不相容分解的多批样板空间,例如移动物体。在这样的情况下,迫击炮被证明是有利的。这一贡献讨论了在功能空间H(curl)和相应的迫击炮空间中解决Maxwell的方程式所需的适当的B-spline空间。本文件的主要贡献是表明,在需要测量的配方中,如磁体方程式的矢量配方,人们可以通过树木分解的图形理论概念将离子内核空间从迫击炮空间中去除。树木-树的分解基于控制网格进行,用于非可承包域,可以直接应用,而不受B-spline基础的程度影响。最后,模拟工作流程是使用一个旋转永久磁性同步机器的现实模型演示的。