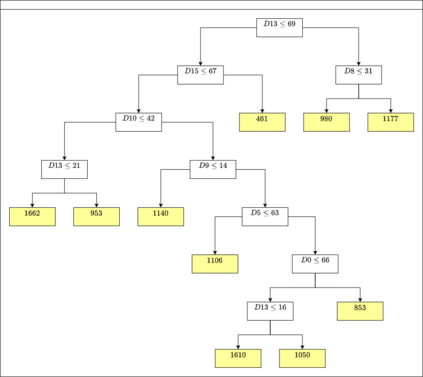
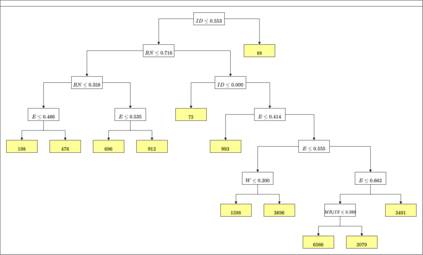
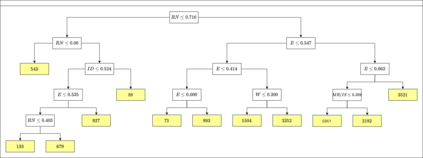
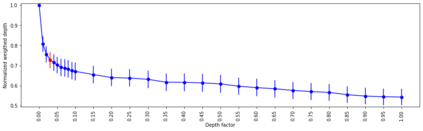
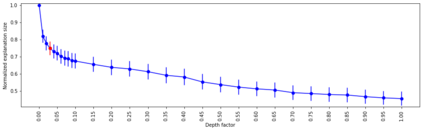
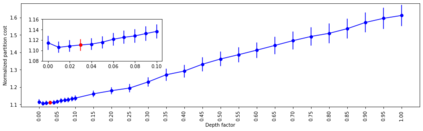
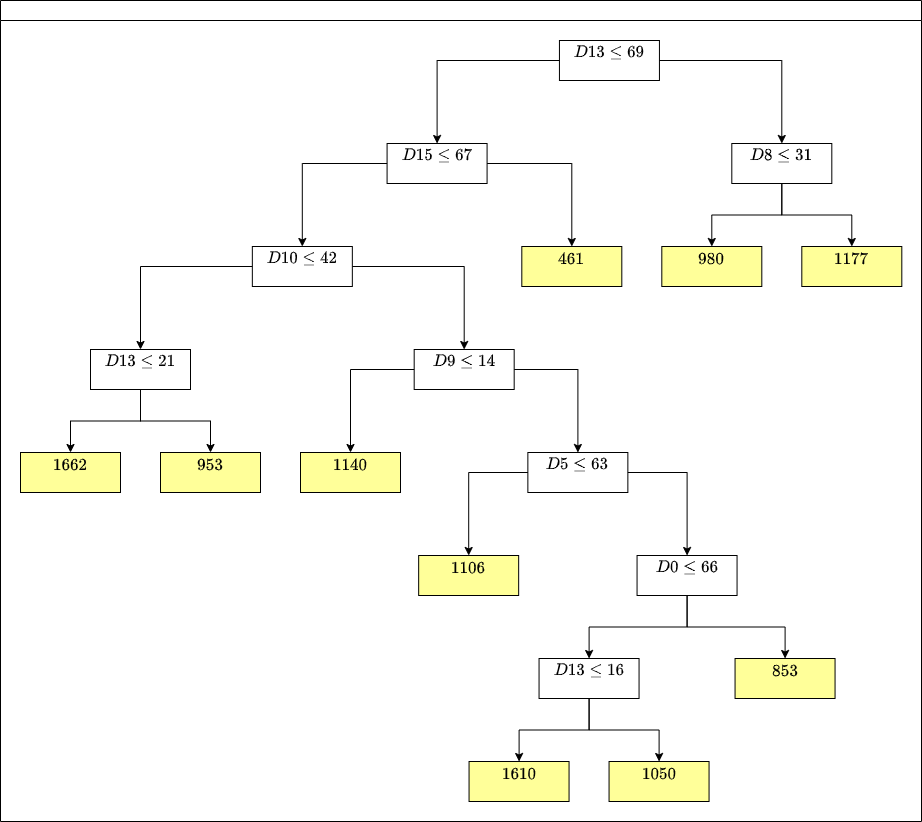
A number of recent works have employed decision trees for the construction of explainable partitions that aim to minimize the $k$-means cost function. These works, however, largely ignore metrics related to the depths of the leaves in the resulting tree, which is perhaps surprising considering how the explainability of a decision tree depends on these depths. To fill this gap in the literature, we propose an efficient algorithm that takes into account these metrics. In experiments on 16 datasets, our algorithm yields better results than decision-tree clustering algorithms such as the ones presented in \cite{dasgupta2020explainable}, \cite{frost2020exkmc}, \cite{laber2021price} and \cite{DBLP:conf/icml/MakarychevS21}, typically achieving lower or equivalent costs with considerably shallower trees. We also show, through a simple adaptation of existing techniques, that the problem of building explainable partitions induced by binary trees for the $k$-means cost function does not admit an $(1+\epsilon)$-approximation in polynomial time unless $P=NP$, which justifies the quest for approximation algorithms and/or heuristics.
翻译:最近的一些工程已经使用决策树来建造可解释的分区,目的是最大限度地减少美元值成本功能。 但是,这些工程基本上忽略了与所产树叶深度有关的测量值, 考虑到决策树的可解释性取决于这些深度, 这也许令人惊讶。 为了填补文献中的这一空白, 我们建议了一个考虑到这些测量值的高效算法。 在16个数据集的实验中, 我们的算法产生的结果优于决策树群集算法, 比如在 $2020202020可探测值 } 、\ cite {frost2020exkm} 、\ cite{frete{laber2021} 和\ cite{DBLP:conf/icml/MakarychevS21} 中呈现出来的那些与较浅的树木相比成本较低或相当的算法。 我们还通过简单调整现有技术, 表明, 建立由双树引发的可解释的分区算法的问题, 例如: $- $- 美元值成本函数 、\ 美元 和 美元- 等值 等值 的算算算值 的 。