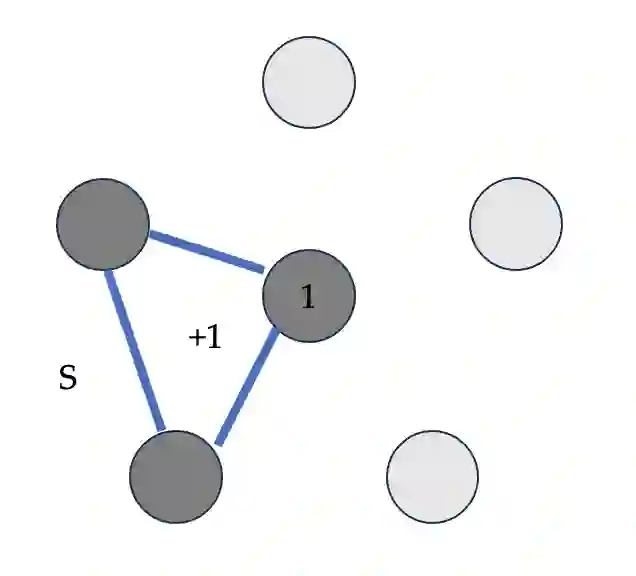
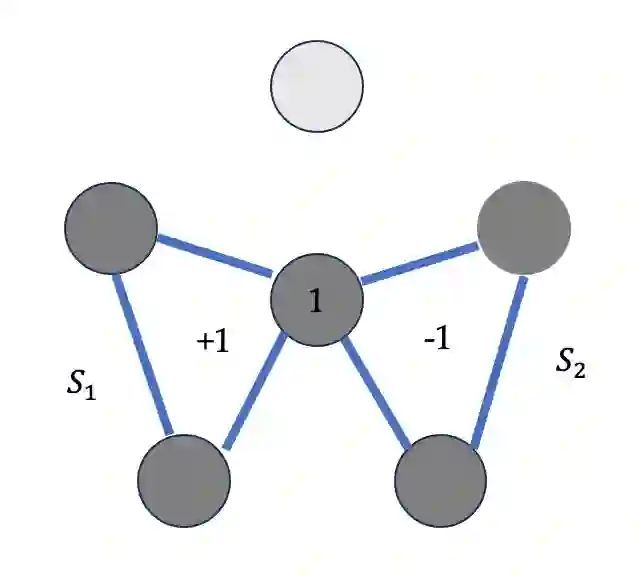
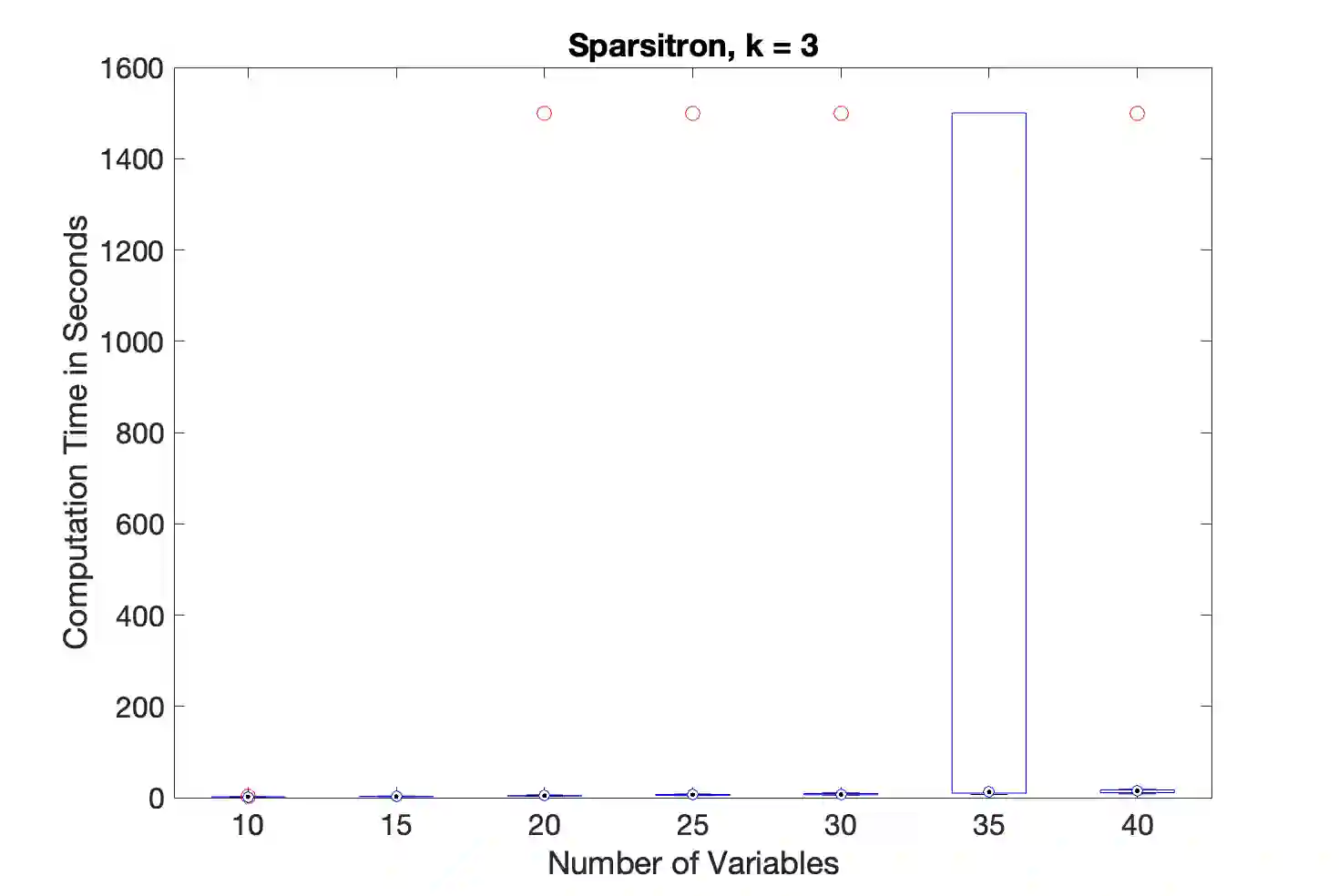
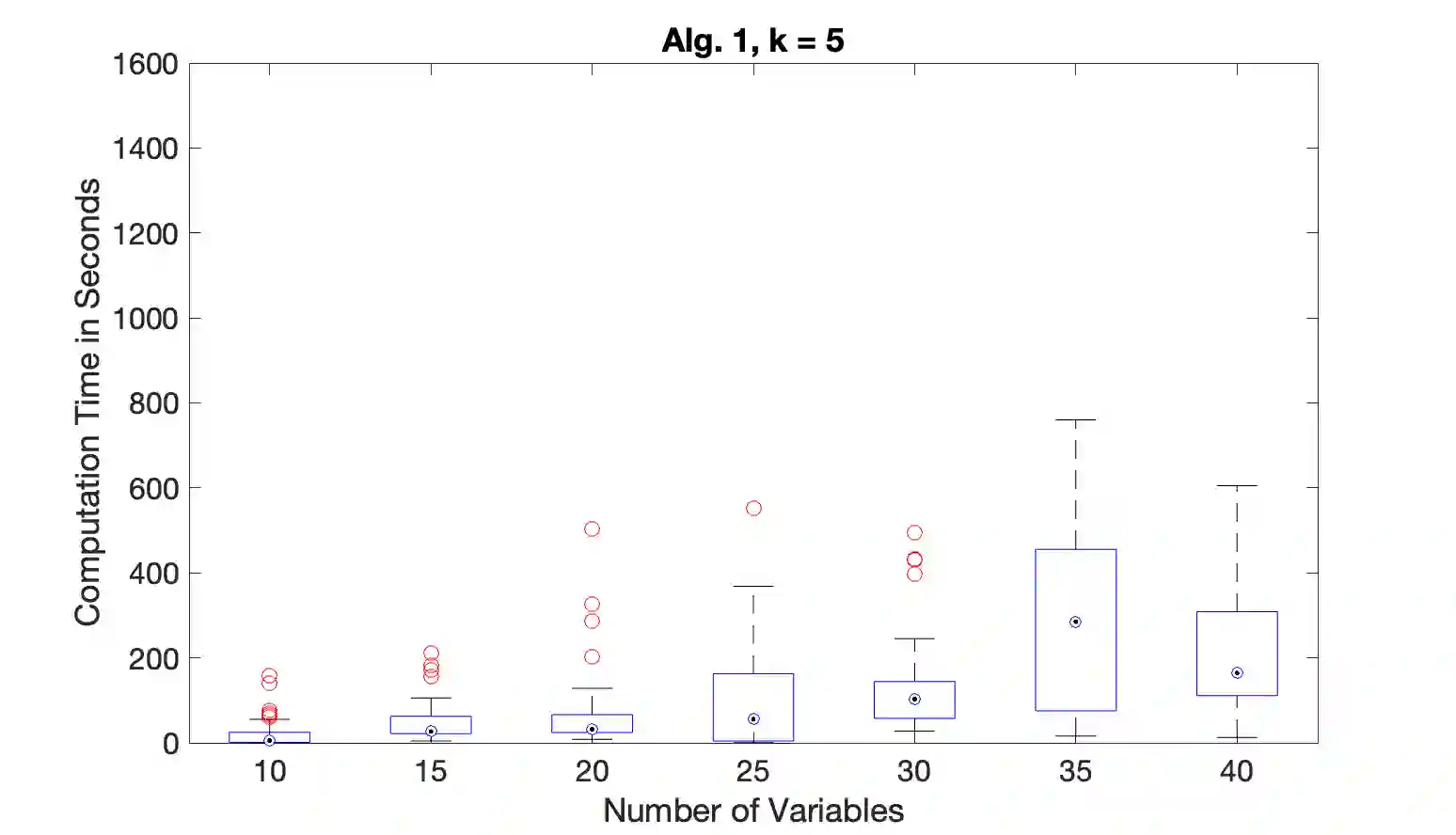
We consider the problem of learning graphical models, also known as Markov random fields (MRFs) from temporally correlated samples. As in many traditional statistical settings, fundamental results in the area all assume independent samples from the distribution. However, these samples generally will not directly correspond to more realistic observations from nature, which instead evolve according to some stochastic process. From the computational lens, even generating a single sample from the true MRF distribution is intractable unless $\mathsf{NP}=\mathsf{RP}$, and moreover, any algorithm to learn from i.i.d. samples requires prohibitive runtime due to hardness reductions to the parity with noise problem. These computational barriers for sampling and learning from the i.i.d. setting severely lessen the utility of these breakthrough results for this important task; however, dropping this assumption typically only introduces further algorithmic and statistical complexities. In this work, we surprisingly demonstrate that the direct trajectory data from a natural evolution of the MRF overcomes the fundamental computational lower bounds to efficient learning. In particular, we show that given a trajectory with $\widetilde{O}_k(n)$ site updates of an order $k$ MRF from the Glauber dynamics, a well-studied, natural stochastic process on graphical models, there is an algorithm that recovers the graph and the parameters in $\widetilde{O}_k(n^2)$ time. By contrast, all prior algorithms for learning order $k$ MRFs inherently suffer from $n^{\Theta(k)}$ runtime even in sparse instances due to the reductions to sparse parity with noise. Our results thus surprisingly show that this more realistic, but intuitively less tractable, model for MRFs actually leads to efficiency far beyond what is known and believed to be true in the traditional i.i.d. case.
翻译:暂无翻译