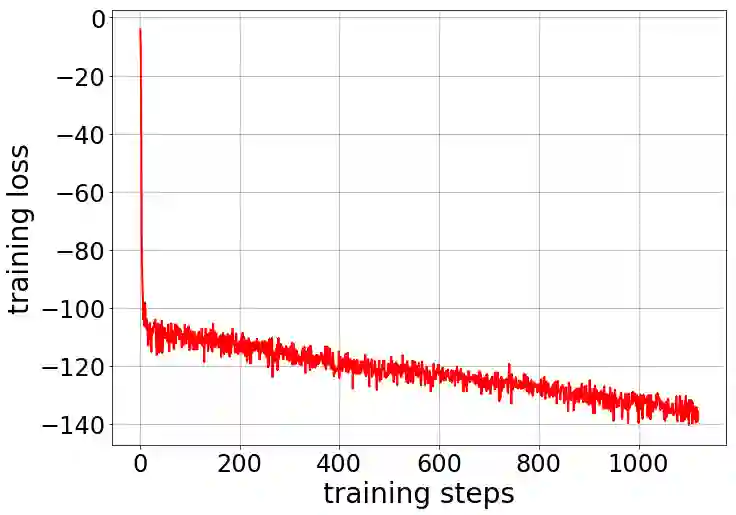
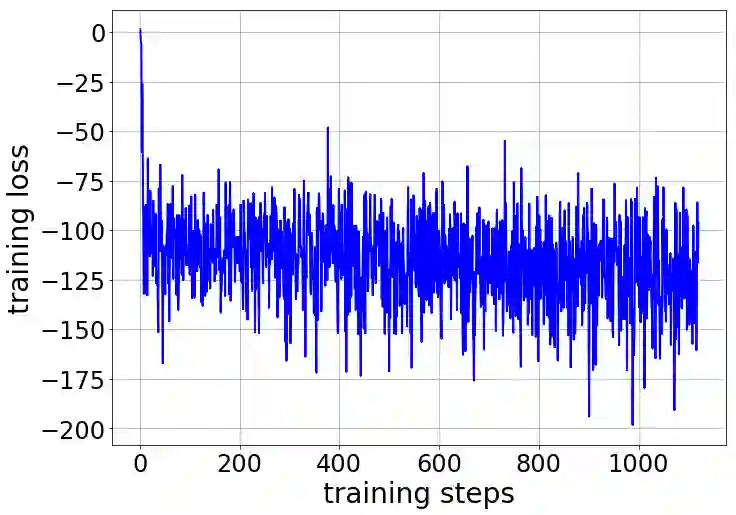
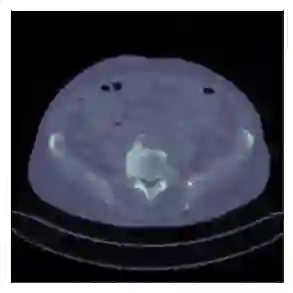
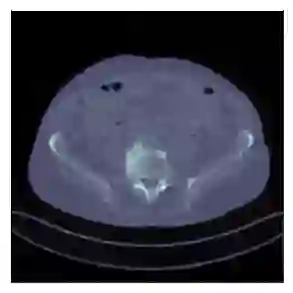
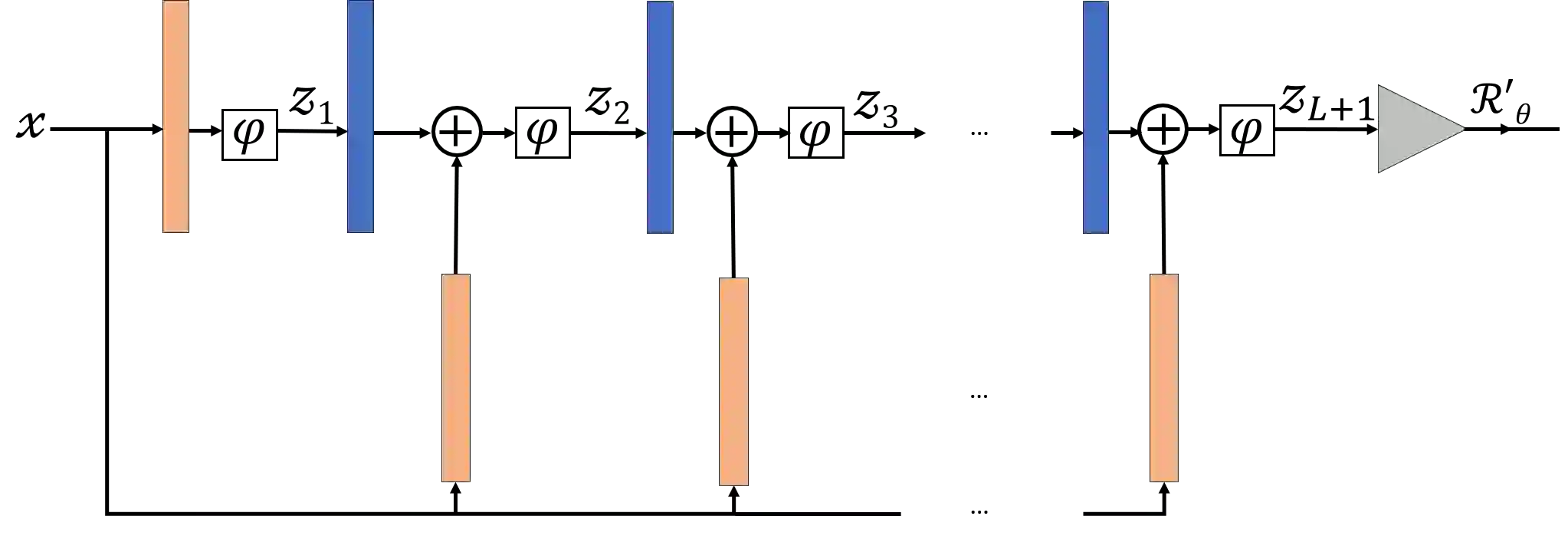We consider the variational reconstruction framework for inverse problems and propose to learn a data-adaptive input-convex neural network (ICNN) as the regularization functional. The ICNN-based convex regularizer is trained adversarially to discern ground-truth images from unregularized reconstructions. Convexity of the regularizer is desirable since (i) one can establish analytical convergence guarantees for the corresponding variational reconstruction problem and (ii) devise efficient and provable algorithms for reconstruction. In particular, we show that the optimal solution to the variational problem converges to the ground-truth if the penalty parameter decays sub-linearly with respect to the norm of the noise. Further, we prove the existence of a sub-gradient-based algorithm that leads to a monotonically decreasing error in the parameter space with iterations. To demonstrate the performance of our approach for solving inverse problems, we consider the tasks of deblurring natural images and reconstructing images in computed tomography (CT), and show that the proposed convex regularizer is at least competitive with and sometimes superior to state-of-the-art data-driven techniques for inverse problems.
翻译:我们认为对反面问题的变异重建框架,并提议学习数据适应输入-convex神经网络(ICNNN)作为正规化功能。基于ICN的 convex正规化器经过对抗性训练,以辨别来自非正规化重建的地面真实图像。常规化器的精确性是可取的,因为(一) 可以为相应的变异重建问题建立分析趋同保障,(二) 为重建设计高效和可辨别的算法。特别是,我们表明,如果刑罚参数在噪音规范方面分线衰减,则变异问题的最佳解决办法会汇合地面真相。此外,我们证明存在着一种亚梯度的算法,导致参数空间中单向减少错误。为了证明我们解决反面问题的方法的性能,我们考虑了在计算成像学中解动自然图像和重建图像(CT)的任务,并表明,拟议的正谱化器对立技术的竞争力最小,有时优于状态驱动的数据问题。