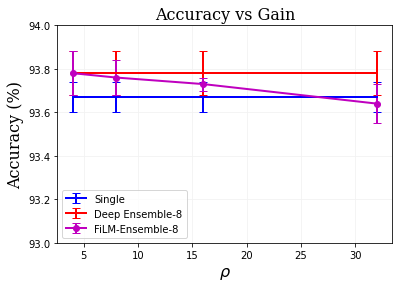
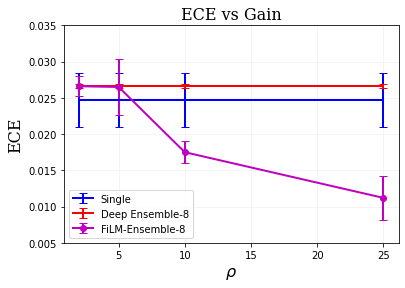
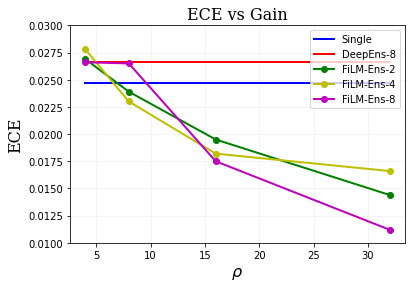
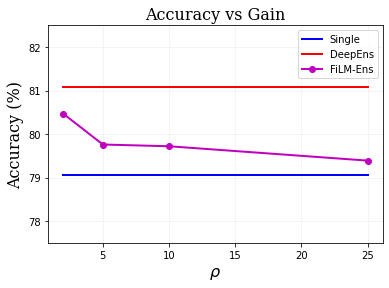
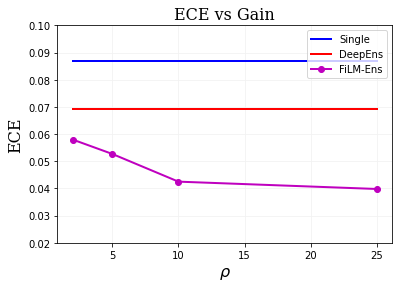
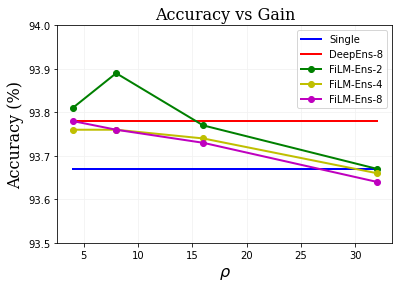
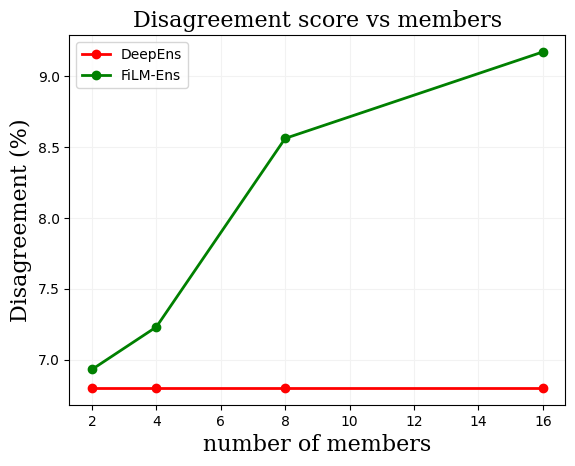
The ability to estimate epistemic uncertainty is often crucial when deploying machine learning in the real world, but modern methods often produce overconfident, uncalibrated uncertainty predictions. A common approach to quantify epistemic uncertainty, usable across a wide class of prediction models, is to train a model ensemble. In a naive implementation, the ensemble approach has high computational cost and high memory demand. This challenges in particular modern deep learning, where even a single deep network is already demanding in terms of compute and memory, and has given rise to a number of attempts to emulate the model ensemble without actually instantiating separate ensemble members. We introduce FiLM-Ensemble, a deep, implicit ensemble method based on the concept of Feature-wise Linear Modulation (FiLM). That technique was originally developed for multi-task learning, with the aim of decoupling different tasks. We show that the idea can be extended to uncertainty quantification: by modulating the network activations of a single deep network with FiLM, one obtains a model ensemble with high diversity, and consequently well-calibrated estimates of epistemic uncertainty, with low computational overhead in comparison. Empirically, FiLM-Ensemble outperforms other implicit ensemble methods, and it and comes very close to the upper bound of an explicit ensemble of networks (sometimes even beating it), at a fraction of the memory cost.
翻译:在现实世界中部署机器学习时,估计隐含不确定性的能力往往至关重要,但在现实世界中,现代方法往往会产生过度自信、未经校正的不确定性预测。一种用于在广泛的预测模型中量化隐含不确定性的常见方法,是培训一个模型组合。在天真的实施中,混合方法具有很高的计算成本和高记忆需求。这种挑战在现代深层次学习中尤为重要,即使是一个深层次的网络在计算和记忆方面都已经要求很高,并导致一些尝试在不实际使单独的混合成员即时地模仿模型组合。我们采用基于精密线性模型概念的深层隐含串联的方法来量化隐含不确定性。这种技术最初是为多功能学习而开发的,目的是解析不同任务。我们表明,这种想法可以扩大到不确定性的量化:通过一个单一的深层次网络的激活,而实际上不易实现单独混合的混合成员。我们引入了一个基于高性线性线性模型的深度混合方法,一种深度的隐含的混合方法,一个在高层次的模型中,一个具有高层次的内定的内存的内存的内存的内存方法。