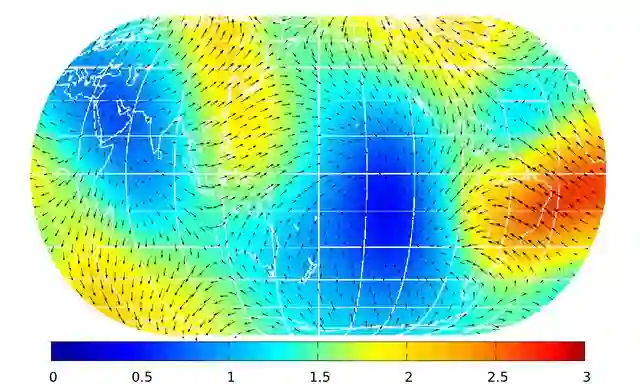
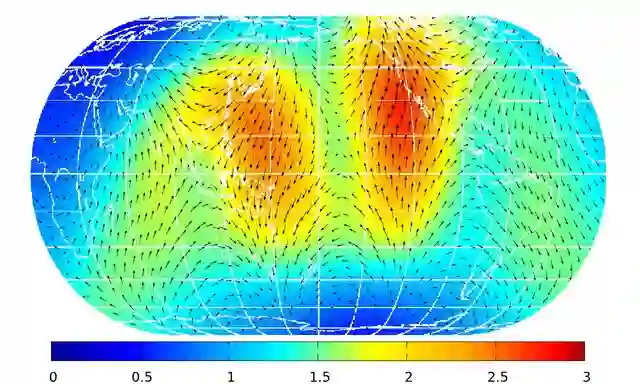
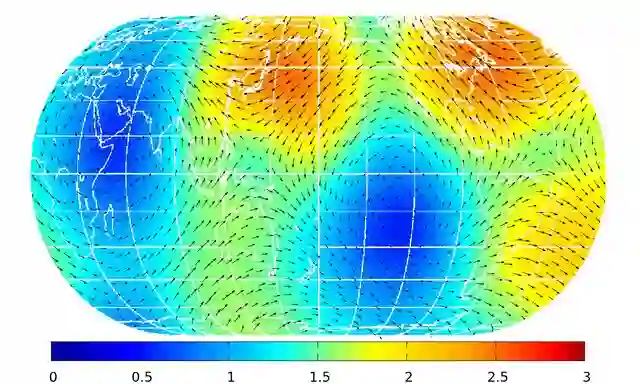
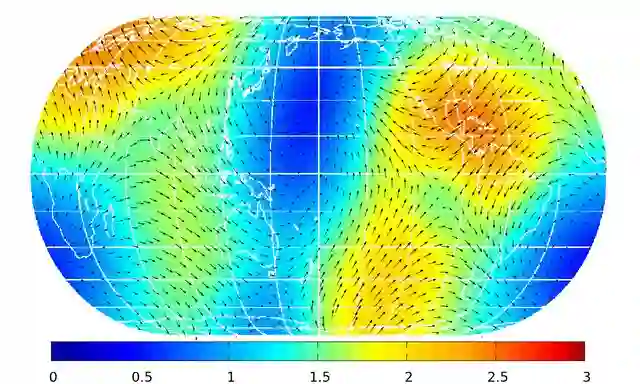
In this work, we develop a high-order collocation method using radial basis function (RBF) for the incompressible Navier-Stokes equation (NSE) on the rotating sphere. The method is based on solving the projection of the NSE on the space of divergence-free functions. For that, we use matrix valued kernel functions which allow an analytically divergence-free approximation of the velocity field. Using kernel functions which lead to rotation-free approximations, the pressure can be recovered by a simple kernel exchange in one of the occurring approximations, without solving an additional Poisson problem. We establish precise error estimates for the velocity and the pressure functions for the semi-discretised solution. In the end, we give a short estimate of the numerical cost and apply the new method to an experimental test case.
翻译:在这项工作中,我们开发了一种高顺序合用法,使用射线基函数(RBF),用于旋转场上不可压缩的纳维-斯托克斯方程式(NSE),该方法基于解决NSE在无差异函数空间上的预测。为此,我们使用矩阵值值的内核函数,从而可以对速度场进行无差异的分析近似。使用导致无旋转近似的内核函数,压力可以通过一个正在发生的近似点中的简单的内核交换来恢复,而不解决额外的 Poisson 问题。我们为半分解溶液的速度和压力函数确定精确的误差估计。最后,我们简要估计了数字成本,并将新方法应用于一个实验性测试案例。