The Power of Small Coalitions under Two-Tier Majority on Regular Graphs

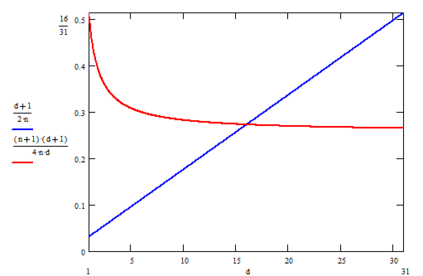
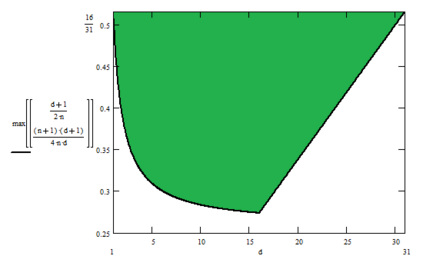
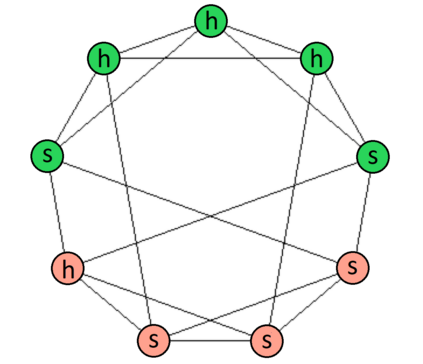
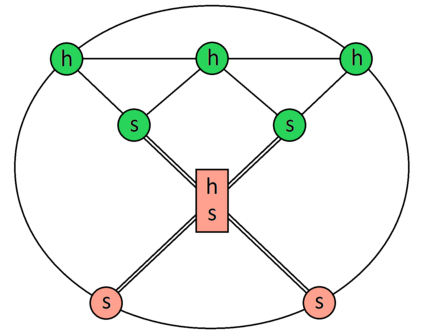
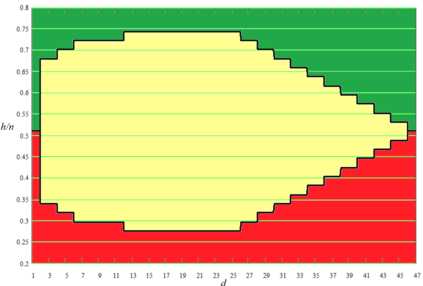
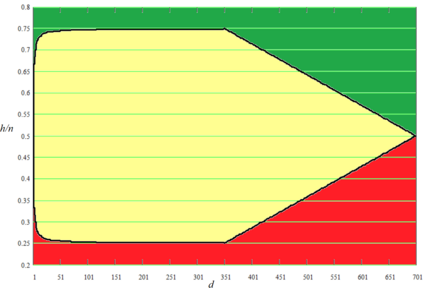
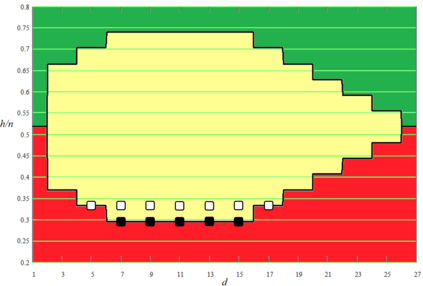
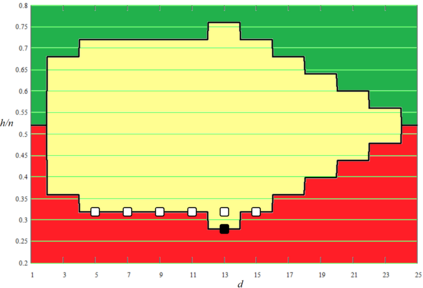
In this paper, we study the following problem. Consider a setting where a proposal is offered to the vertices of a given network $G$, and the vertices must conduct a vote and decide whether to accept the proposal or reject it. Each vertex $v$ has its own valuation of the proposal; we say that $v$ is ``happy'' if its valuation is positive (i.e., it expects to gain from adopting the proposal) and ``sad'' if its valuation is negative. However, vertices do not base their vote merely on their own valuation. Rather, a vertex $v$ is a \emph{proponent} of the proposal if a majority of its neighbors are happy with it and an \emph{opponent} in the opposite case. At the end of the vote, the network collectively accepts the proposal whenever a majority of its vertices are proponents. We study this problem on regular graphs with loops. Specifically, we consider the class ${\mathcal G}_{n|d|h}$ of $d$-regular graphs of odd order $n$ with all $n$ loops and $h$ happy vertices. We are interested in establishing necessary and sufficient conditions for the class ${\mathcal G}_{n|d|h}$ to contain a labeled graph accepting the proposal, as well as conditions to contain a graph rejecting the proposal. We also discuss connections to the existing literature, including that on majority domination, and investigate the properties of the obtained conditions.