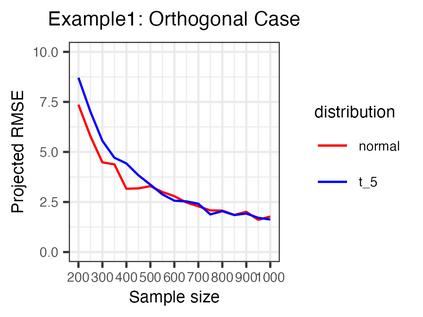
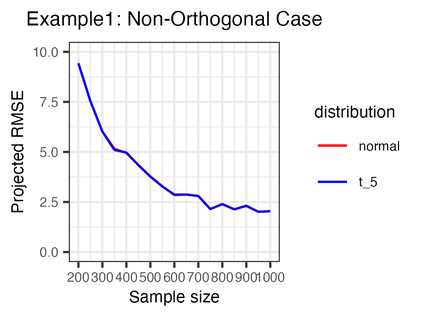
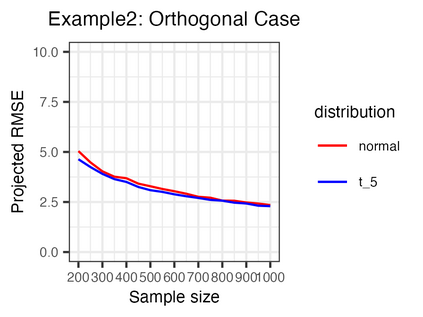
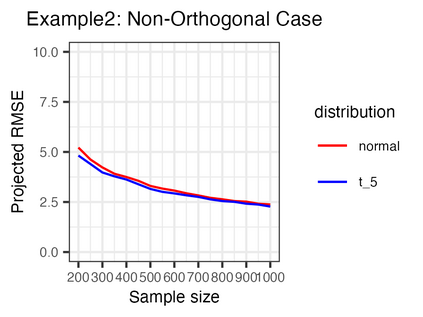
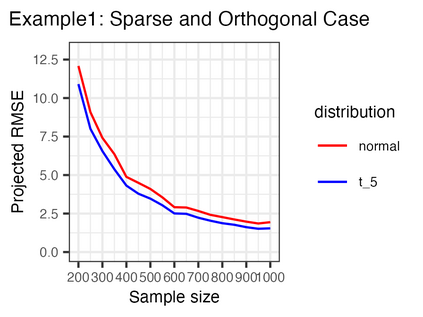
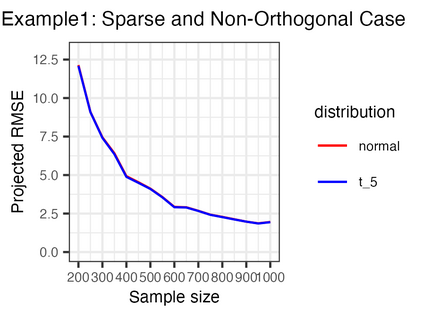
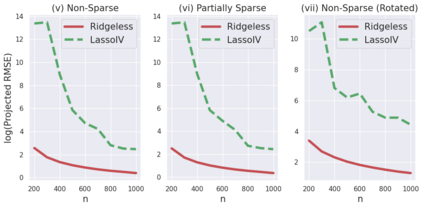
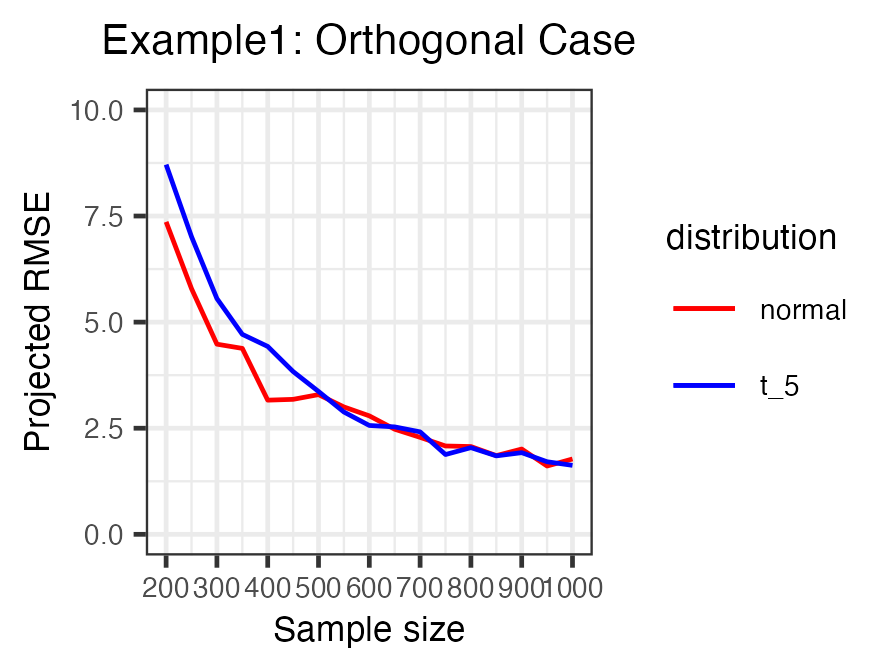
We investigate the high-dimensional linear regression problem in the presence of noise correlated with Gaussian covariates. This correlation, known as endogeneity in regression models, often arises from unobserved variables and other factors. It has been a major challenge in causal inference and econometrics. When the covariates are high-dimensional, it has been common to assume sparsity on the true parameters and estimate them using regularization, even with the endogeneity. However, when sparsity does not hold, it has not been well understood to control the endogeneity and high dimensionality simultaneously. This study demonstrates that an estimator without regularization can achieve consistency, that is, benign overfitting, under certain assumptions on the covariance matrix. Specifically, our results show that the error of this estimator converges to zero when the covariance matrices of correlated noise and instrumental variables satisfy a condition on their eigenvalues. We consider several extensions relaxing these conditions and conduct experiments to support our theoretical findings. As a technical contribution, we utilize the convex Gaussian minimax theorem (CGMT) in our dual problem and extend CGMT itself.
翻译:暂无翻译