Multiple Testing and Variable Selection along Least Angle Regression's path

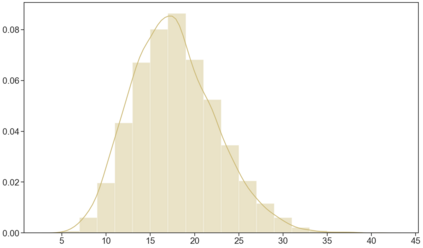
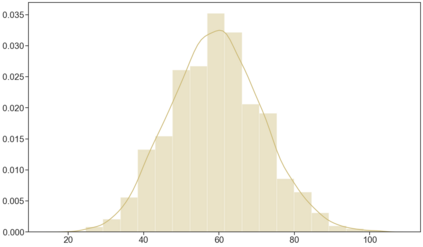
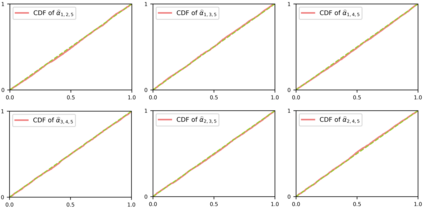
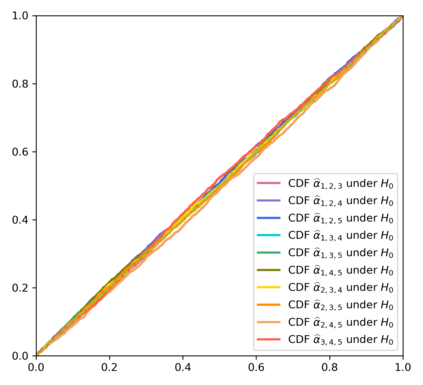
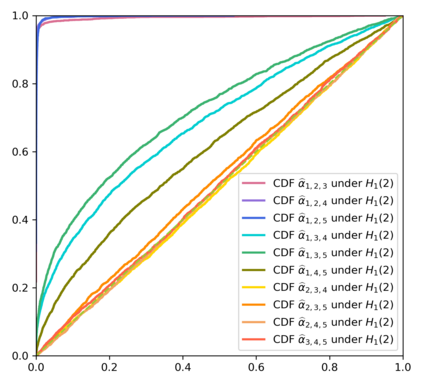
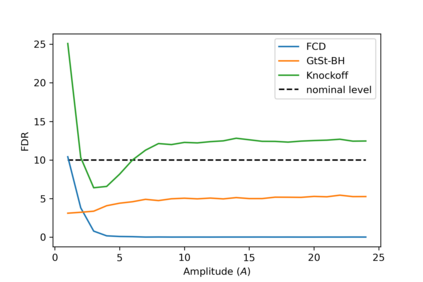
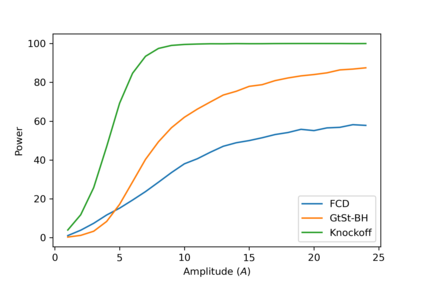
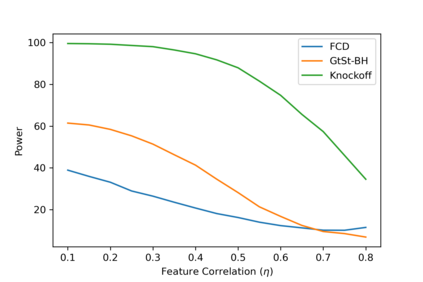
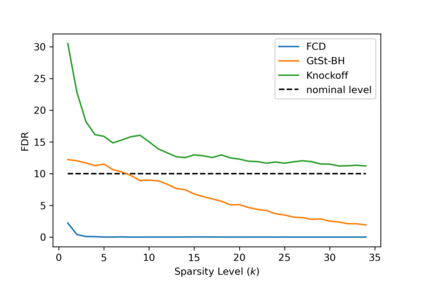
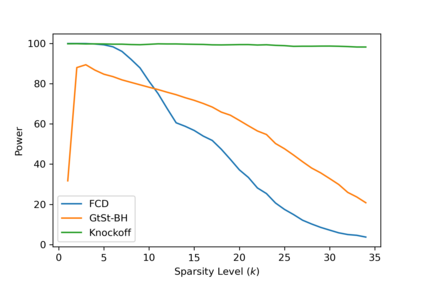
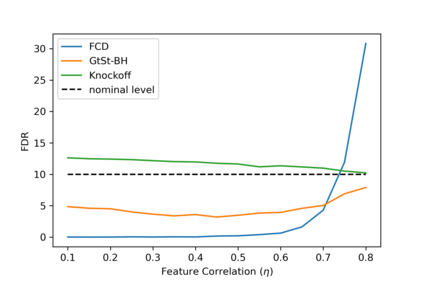
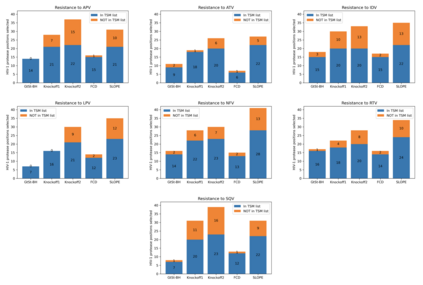
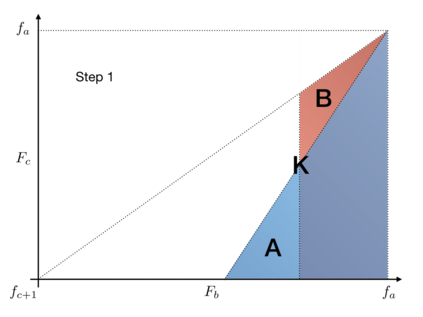
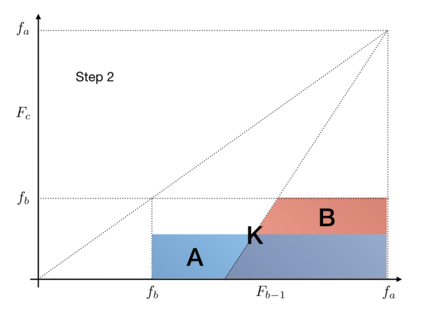
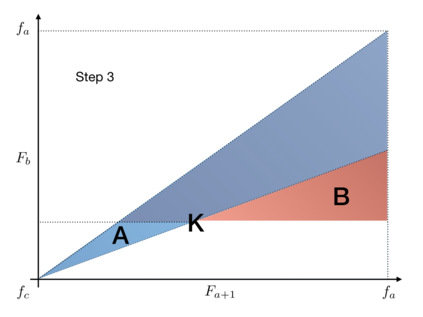
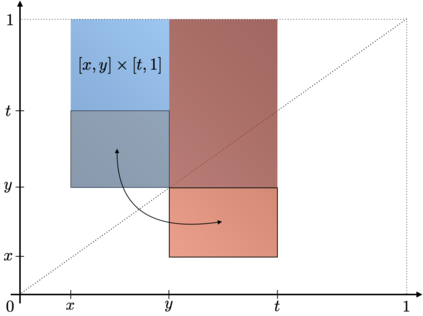
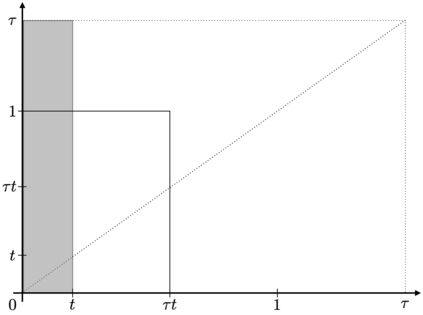
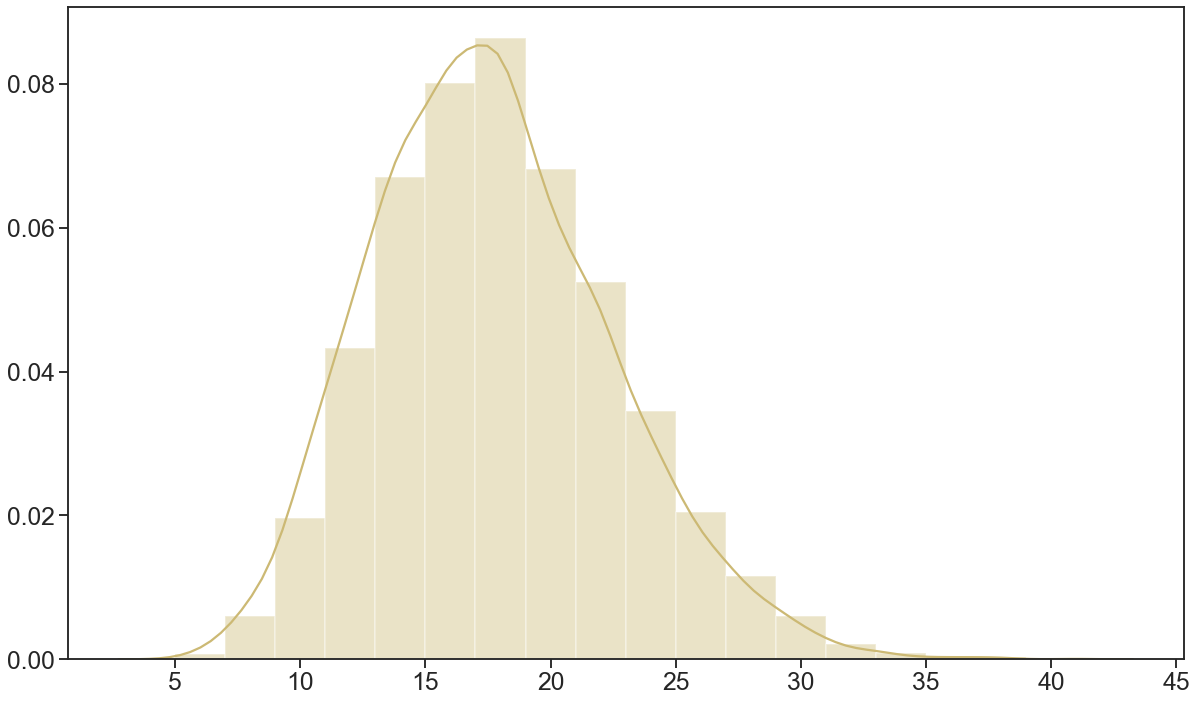
In this article, we investigate multiple testing and variable selection using Least Angle Regression (LARS) algorithm in high dimensions under the Gaussian noise assumption. LARS is known to produce a piecewise affine solutions path with change points referred to as knots of the LARS path. The cornerstone of the present work is the expression in closed form of the exact joint law of K-uplets of knots conditional on the variables selected by LARS, namely the so-called post-selection joint law of the LARS knots. Numerical experiments demonstrate the perfect fit of our finding. Our main contributions are three fold. First, we build testing procedures on variables entering the model along the LARS path in the general design case when the noise level can be unknown. This testing procedures are referred to as the Generalized t-Spacing tests (GtSt) and we prove that they have exact non-asymptotic level (i.e., Type I error is exactly controlled). In that way, we extend a work from (Taylor et al., 2014) where the Spacing test works for consecutive knots and known variance. Second, we introduce a new exact multiple false negatives test after model selection in the general design case when the noise level can be unknown. We prove that this testing procedure has exact non-asymptotic level for general design and unknown noise level. Last, we give an exact control of the false discovery rate (FDR) under orthogonal design assumption. Monte-Carlo simulations and a real data experiment are provided to illustrate our results in this case. Of independent interest, we introduce an equivalent formulation of LARS algorithm based on a recursive function.