Arbitration-Free Consistency is Available (and Vice Versa)

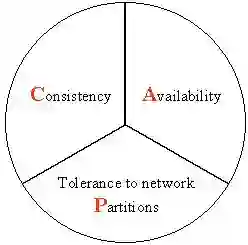
The fundamental tension between \emph{availability} and \emph{consistency} shapes the design of distributed storage systems. Classical results capture extreme points of this trade-off: the CAP theorem shows that strong models like linearizability preclude availability under partitions, while weak models like causal consistency remain implementable without coordination. These theorems apply to simple read-write interfaces, leaving open a precise explanation of the combinations of object semantics and consistency models that admit available implementations. This paper develops a general semantic framework in which storage specifications combine operation semantics and consistency models. The framework encompasses a broad range of objects (key-value stores, counters, sets, CRDTs, and transactional databases) and consistency models (from causal consistency and sequential consistency to snapshot isolation and transactional and non-transactional SQL). Within this framework, we prove the \emph{Arbitration-Free Consistency} (AFC) theorem, showing that an object specification within a consistency model admits an available implementation if and only if it is \emph{arbitration-free}, that is, it does not require a total arbitration order to resolve visibility or read dependencies. The AFC theorem unifies and generalizes previous results, revealing arbitration-freedom as the fundamental property that delineates coordination-free consistency from inherently synchronized behavior.