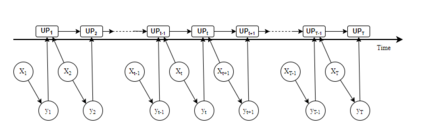
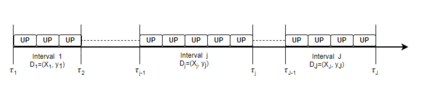
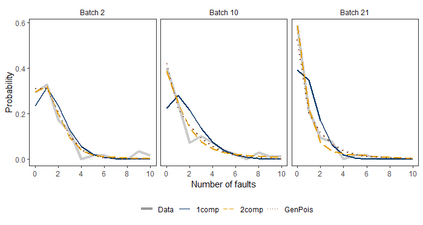
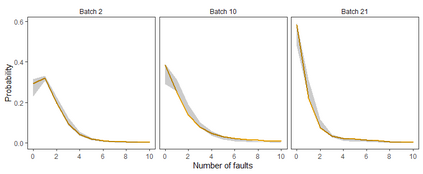
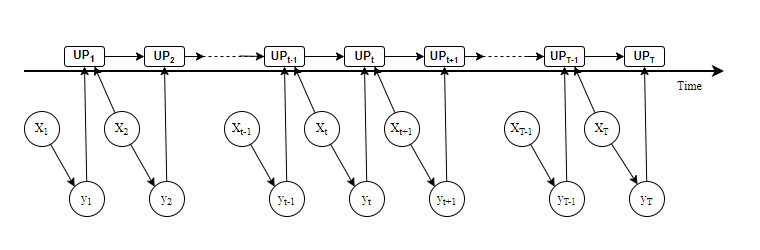
A mixture of experts models the conditional density of a response variable using a mixture of regression models with covariate-dependent mixture weights. We extend the finite mixture of experts model by allowing the parameters in both the mixture components and the weights to evolve in time by following random walk processes. Inference for time-varying parameters in richly parameterized mixture of experts models is challenging. We propose a sequential Monte Carlo algorithm for online inference and based on a tailored proposal distribution built on ideas from linear Bayes methods and the EM algorithm. The method gives a unified treatment for mixtures with time-varying parameters, including the special case of static parameters. We assess the properties of the method on simulated data and on industrial data where the aim is to predict software faults in a continuously upgraded large-scale software project.
翻译:一种专家混合模型,用一种回归模型与共变量依赖混合物重量的混合体来模拟响应变量的有条件密度。我们通过允许混合成分的参数和重量的参数通过随机行走过程而随着时间的演变来扩展专家的有限混合模型。在丰富参数化的专家混合模型中,时间变化参数的推论具有挑战性。我们提出在线推论的连续蒙特卡洛算法,并以基于线性贝斯法和EM算法设想的量身定制的建议分布为基础。该方法对配有时间变化参数的混合物,包括静态参数的特殊情况,进行统一处理。我们评估模拟数据和工业数据方法的特性,目的是预测不断升级的大型软件项目的软件缺陷。