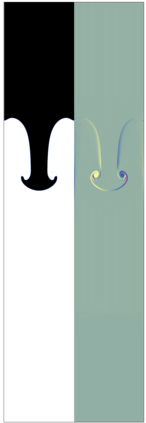
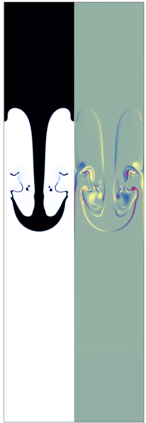
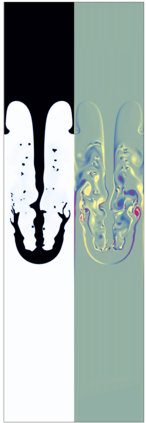
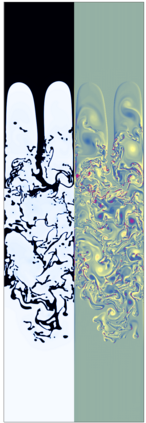
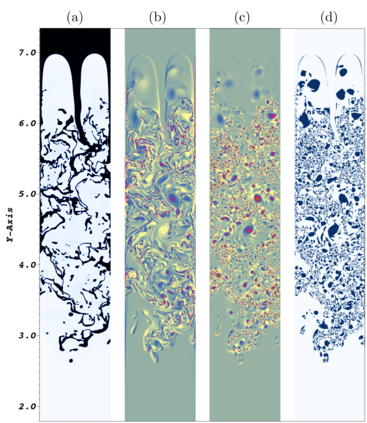
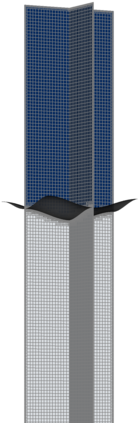
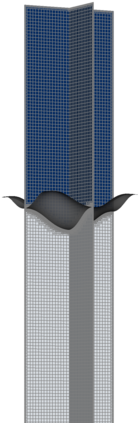
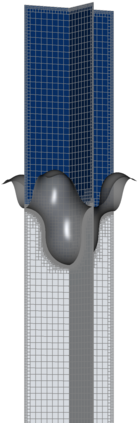
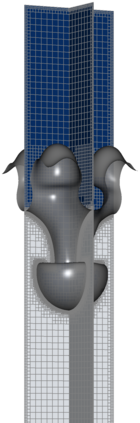
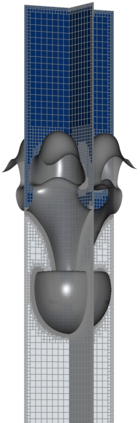
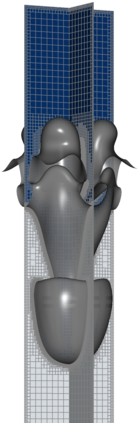
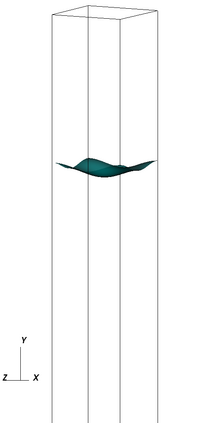
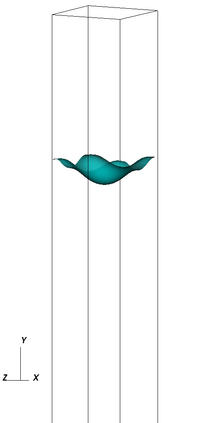
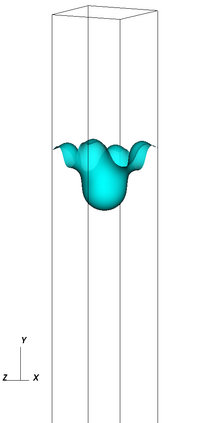
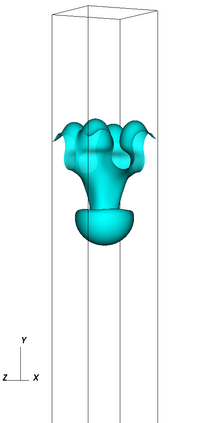
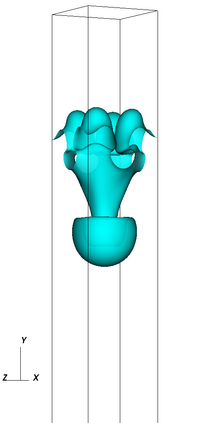
The Cahn-Hilliard Navier-Stokes (CHNS) system provides a computationally tractable model that can be used to effectively capture interfacial dynamics in two-phase fluid flows. In this work, we present a semi-implicit, projection-based finite element framework for solving the CHNS system. We use a projection-based semi-implicit time discretization for the Navier-Stokes equation and a fully-implicit time discretization for the Cahn-Hilliard equation. We use a conforming continuous Galerkin (cG) finite element method in space equipped with a residual-based variational multiscale (RBVMS) formulation. Pressure is decoupled using a projection step, which results in two linear positive semi-definite systems for velocity and pressure, instead of the saddle point system of a pressure-stabilized method. All the linear systems are solved using an efficient and scalable algebraic multigrid (AMG) method. We deploy this approach on a massively parallel numerical implementation using parallel octree-based adaptive meshes. The overall approach allows the use of relatively large time steps with much faster time-to-solve than similar fully-implicit methods. We present comprehensive numerical experiments showing detailed comparisons with results from the literature for canonical cases, including the single bubble rise and Rayleigh-Taylor instability.
翻译:Cahn-Hilliard Navier-Stokes (CHNS) 系统提供了一种可计算化的模型,可用于在两阶段流流中有效捕捉跨度动态。 在这项工作中,我们提出了一个解决 CHNS 系统的半不透明、基于投影的限定元素框架。 我们用一个基于投影的半不透明时间分解系统来解决 Navier-Stokes 等式, 并用一个完全不显眼的时间分解法来解决 Cahn-Hilliard 等式。 我们在空间使用一个符合连续的 Galerkin (c G) 有限元素方法, 配有基于残余的多级变异性( RBVMS) 配制。 压力是用一个预测步骤拆分解的, 从而形成两个直线的半非固定值的半固定值元素框架框架, 而不是压力稳定方法的支撑点。 所有线性系统都是用一个高效且可变缩缩的多格(AMG) 方法解决的。 我们用这个方法在大规模平行的数字执行上应用这个方法, 使用一个平行的基于子调整的多尺度的多级的多级的多级(RBIS),, 和整个方法可以使用一个相对的模型的 和完整的实验, 我们用一个相对的平的平的平比一个比一个相对的平时空的模型,可以使用一个相对的平的模型, 。