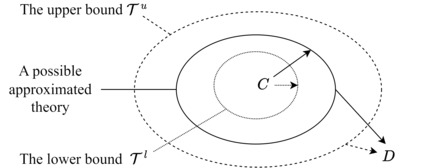
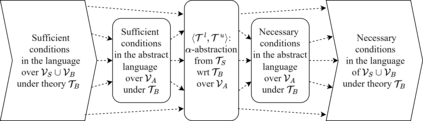
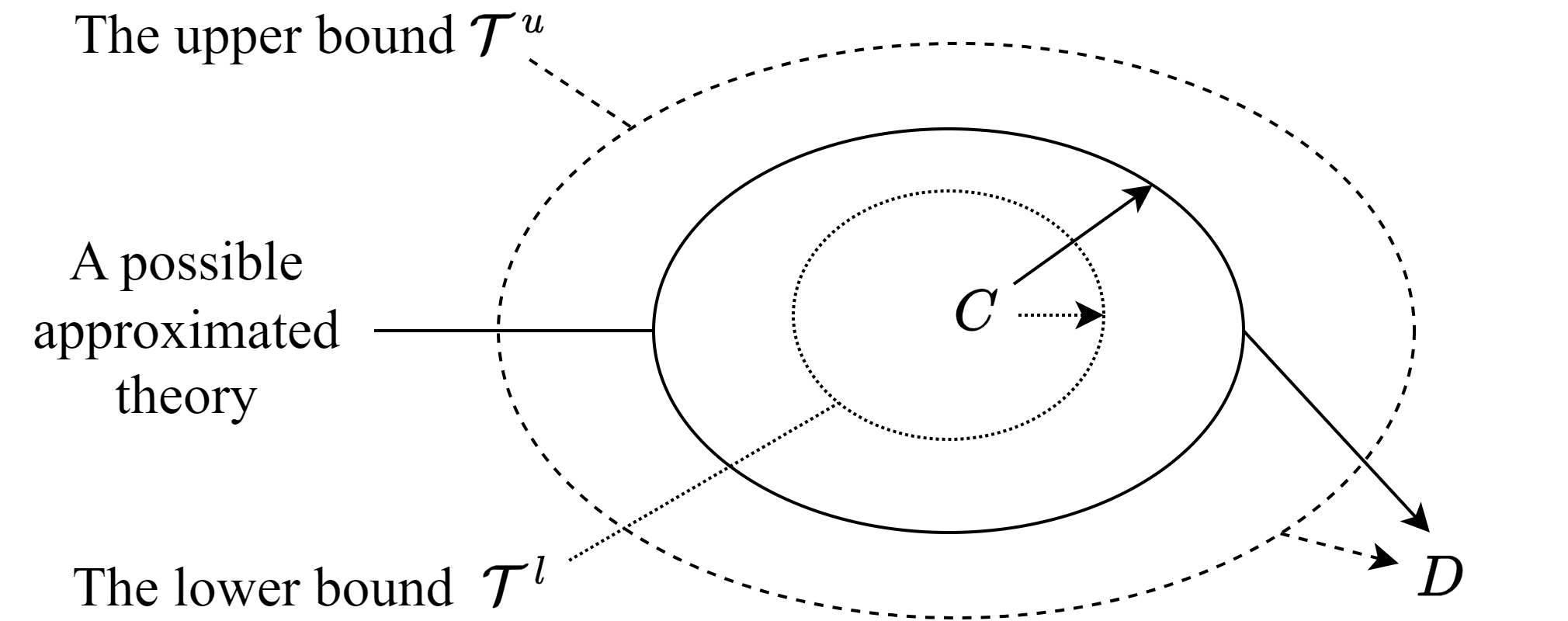
At its core, abstraction is the process of generalizing from specific instances to broader concepts or models, with the primary objective of reducing complexity while preserving properties essential to the intended purpose. It is a fundamental, often implicit, principle that structures the understanding, communication, and development of both scientific knowledge and everyday beliefs. Studies on abstraction have evolved from its origins in Ancient Greek philosophy through methodological approaches in psychological and philosophical theories to computational frameworks. Formally, abstraction can be understood as the transformation of a source representation into an abstract representation that discards certain details while retaining desirable features. In real-world modeling and reasoning, abstraction is crucial, particularly when managing imperfect or incomplete information that calls for approximate representations. This paper introduces a novel logic-based framework for modeling abstraction processes that goes beyond the traditional entailment of necessary conditions to encompass sufficient conditions as well. We define approximate abstractions, study their tightest and exact forms, and extend the approach to layered abstractions, enabling hierarchical simplification of complex systems and models. The computational complexity of the related reasoning tasks is also discussed. For clarity, our framework is developed within classical logic, chosen for its simplicity, expressiveness, and computational friendliness.
翻译:暂无翻译