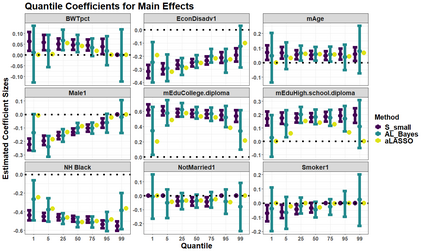
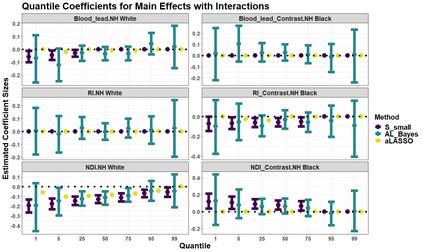
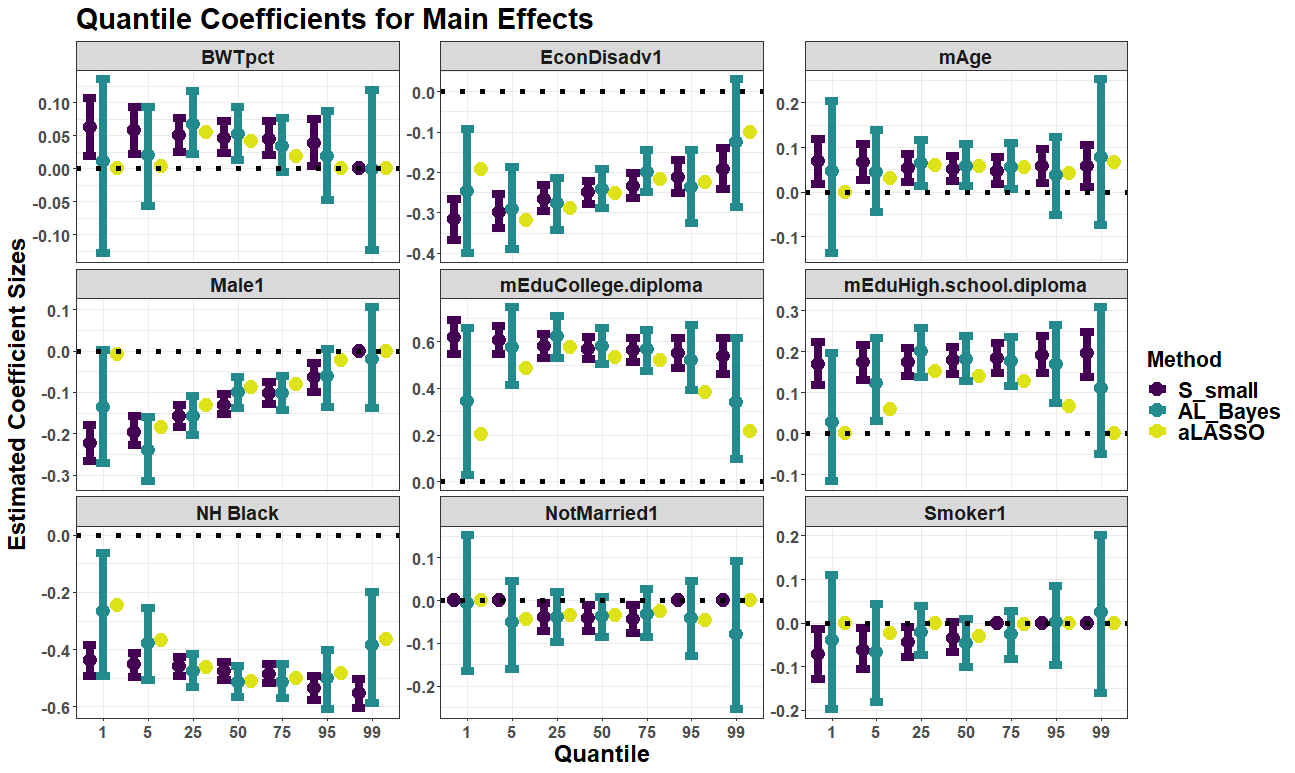
Quantile regression is a powerful tool for inferring how covariates affect specific percentiles of the response distribution. Existing methods either estimate conditional quantiles separately for each quantile of interest or estimate the entire conditional distribution using semi- or non-parametric models. The former often produce inadequate models for real data and do not share information across quantiles, while the latter are characterized by complex and constrained models that can be difficult to interpret and computationally inefficient. Further, neither approach is well-suited for quantile-specific subset selection. Instead, we pose the fundamental problems of linear quantile estimation, uncertainty quantification, and subset selection from a Bayesian decision analysis perspective. For any Bayesian regression model, we derive optimal and interpretable linear estimates and uncertainty quantification for each model-based conditional quantile. Our approach introduces a quantile-focused squared error loss, which enables efficient, closed-form computing and maintains a close relationship with Wasserstein-based density estimation. In an extensive simulation study, our methods demonstrate substantial gains in quantile estimation accuracy, variable selection, and inference over frequentist and Bayesian competitors. We apply these tools to identify the quantile-specific impacts of social and environmental stressors on educational outcomes for a large cohort of children in North Carolina.
翻译:暂无翻译