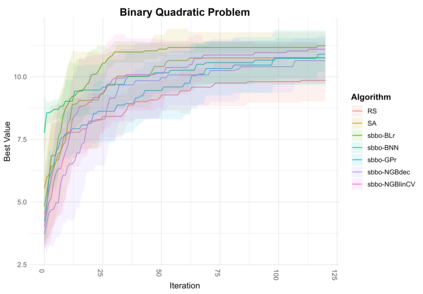
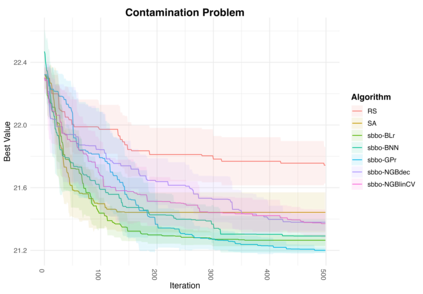
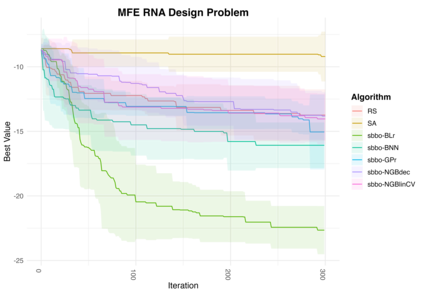
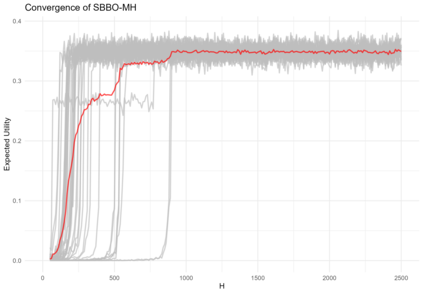
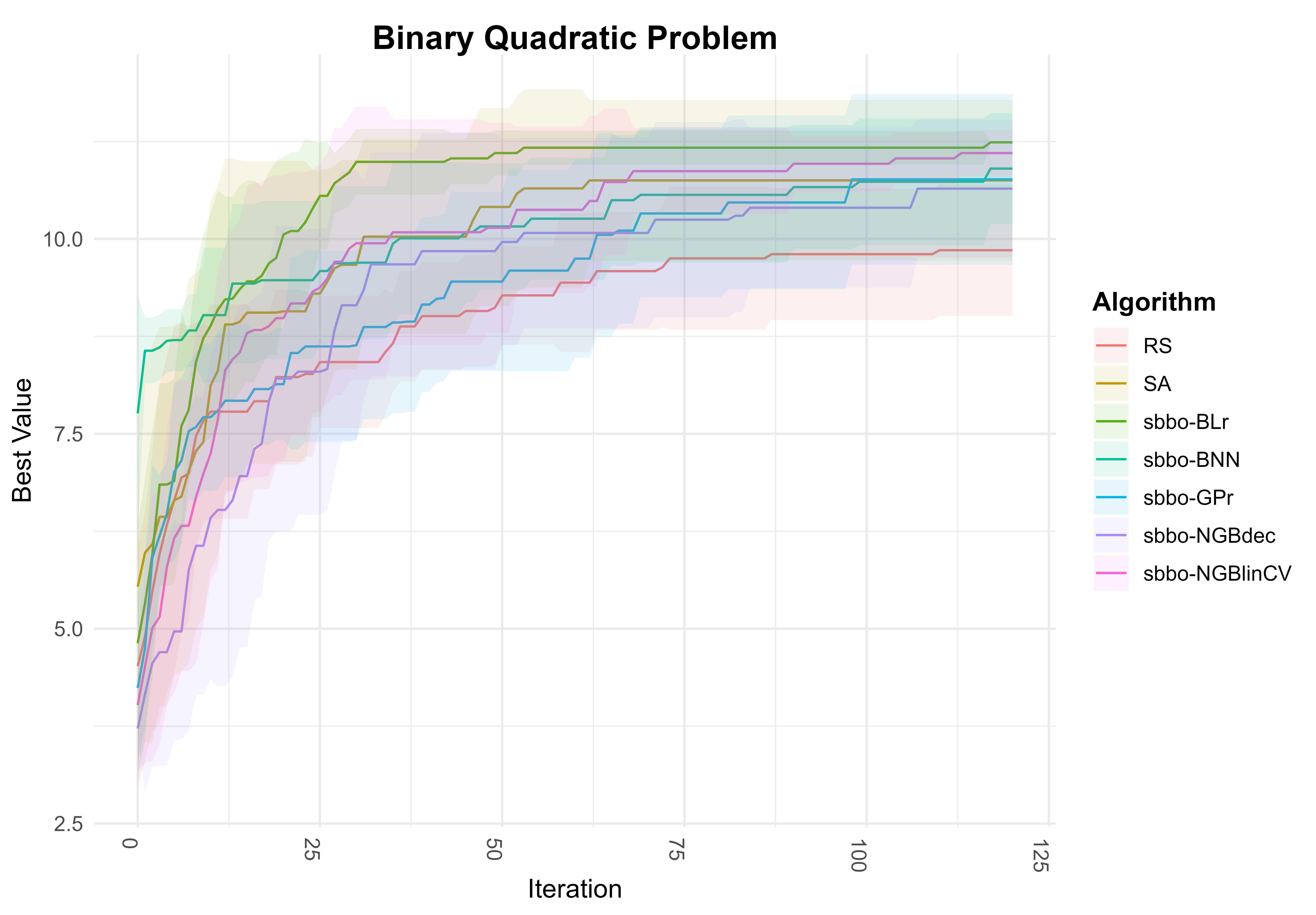
Bayesian Optimization (BO) is a powerful method for optimizing black-box functions by combining prior knowledge with ongoing function evaluations. BO constructs a probabilistic surrogate model of the objective function given the covariates, which is in turn used to inform the selection of future evaluation points through an acquisition function. For smooth continuous search spaces, Gaussian Processes (GPs) are commonly used as the surrogate model as they offer analytical access to posterior predictive distributions, thus facilitating the computation and optimization of acquisition functions. However, in complex scenarios involving optimizations over categorical or mixed covariate spaces, GPs may not be ideal. This paper introduces Simulation Based Bayesian Optimization (SBBO) as a novel approach to optimizing acquisition functions that only requires \emph{sampling-based} access to posterior predictive distributions. SBBO allows the use of surrogate probabilistic models tailored for combinatorial spaces with discrete variables. Any Bayesian model in which posterior inference is carried out through Markov chain Monte Carlo can be selected as the surrogate model in SBBO. In applications involving combinatorial optimization, we demonstrate empirically the effectiveness of SBBO method using various choices of surrogate models.
翻译:暂无翻译