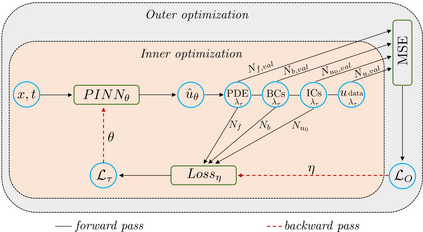
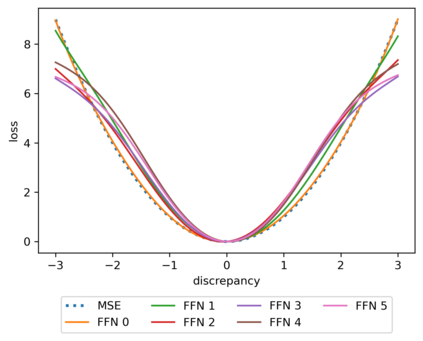
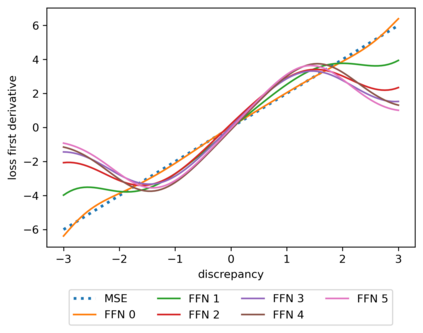
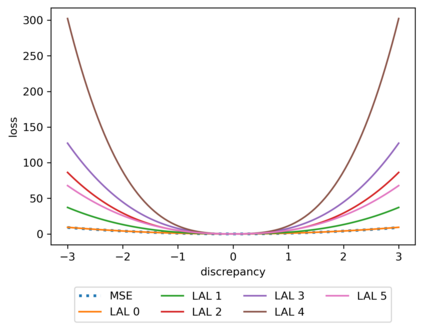
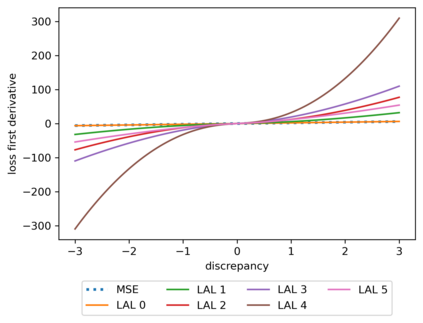
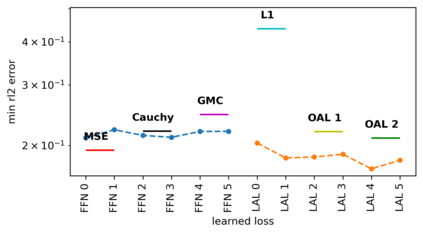
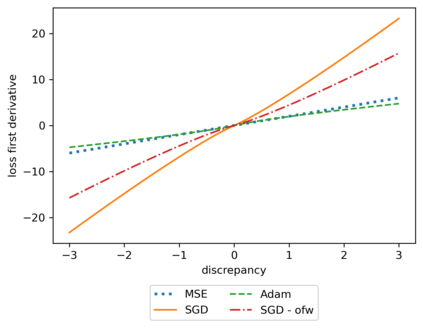
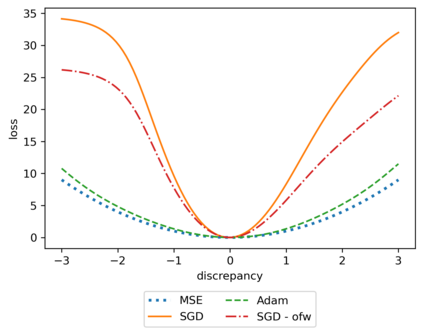
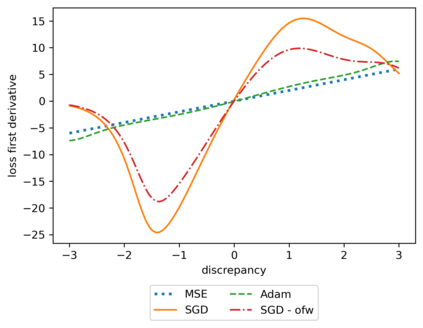
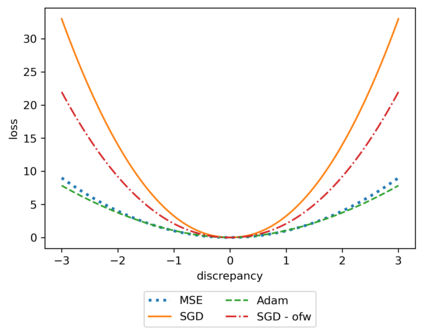
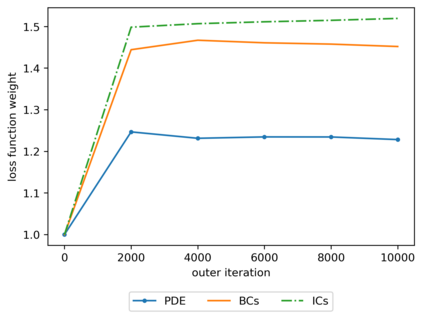
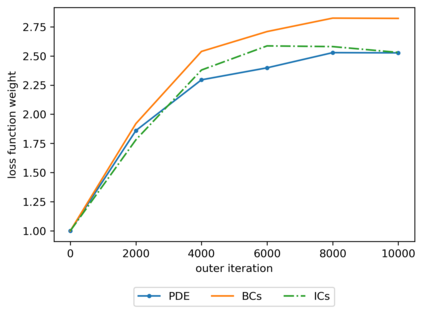
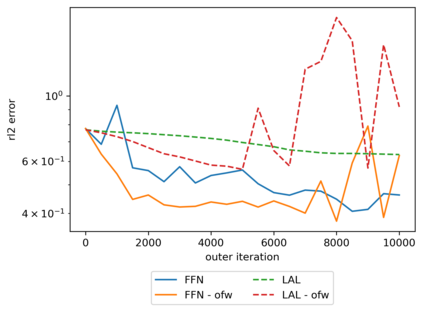
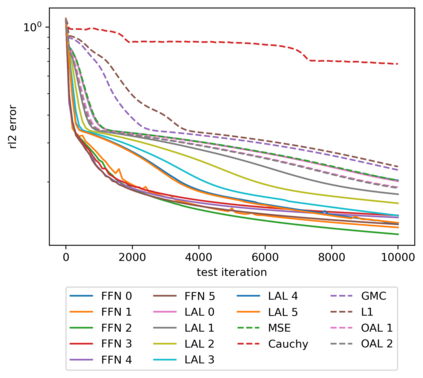
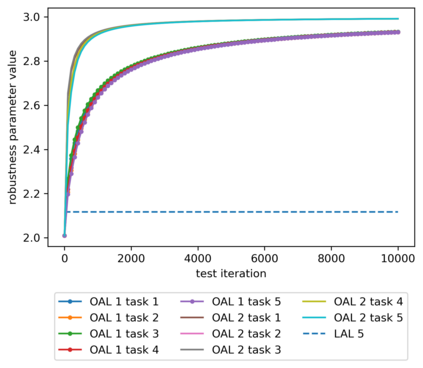
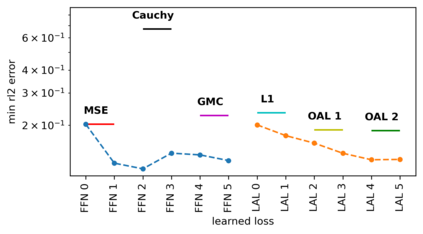
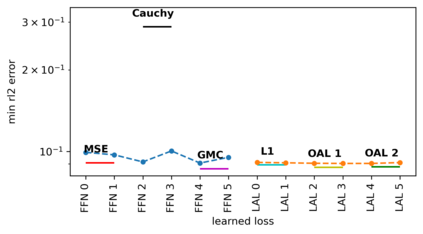
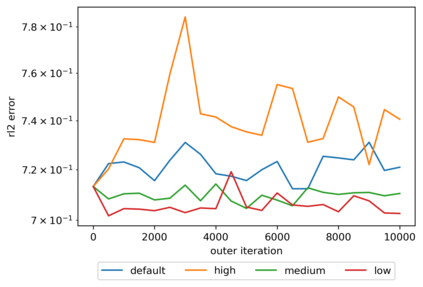
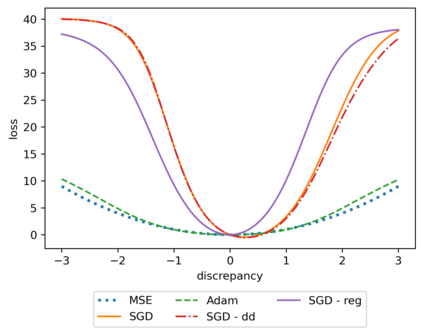
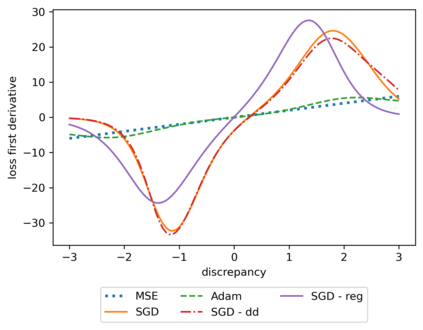
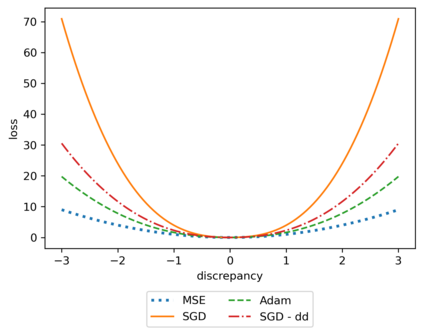
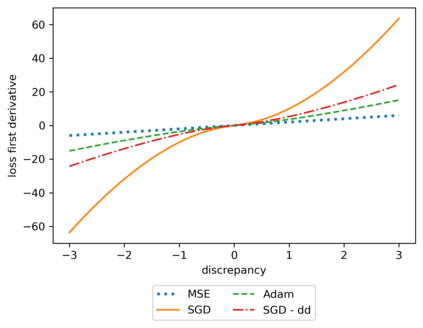
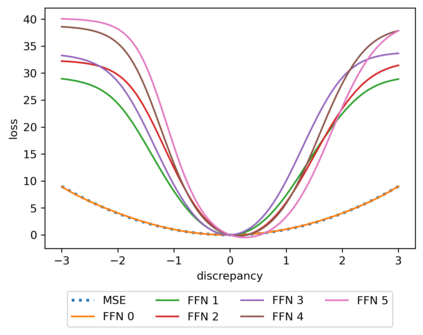
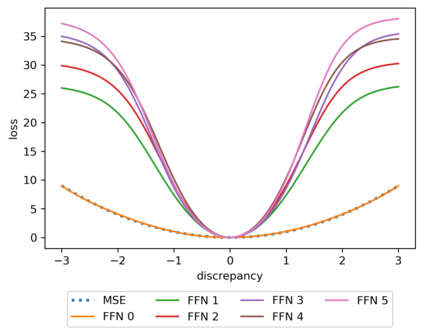
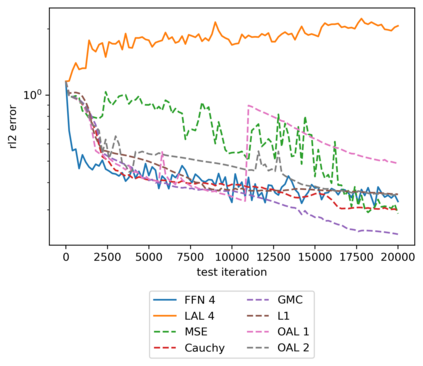
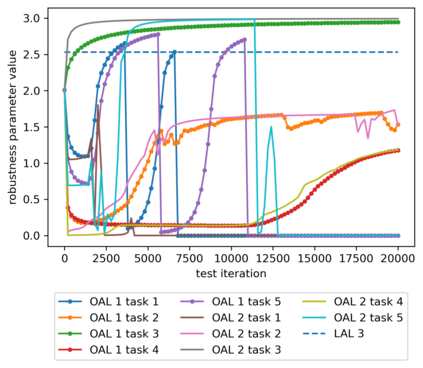
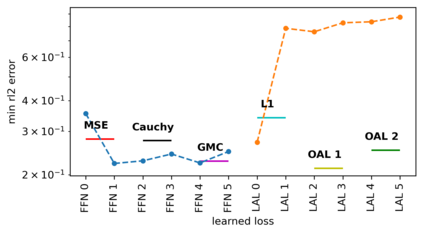
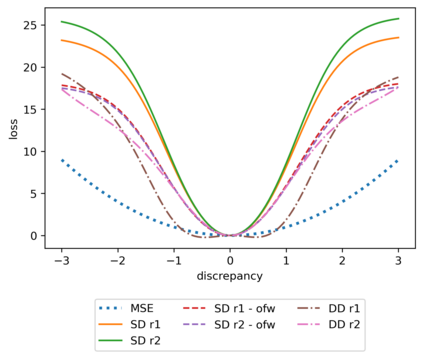
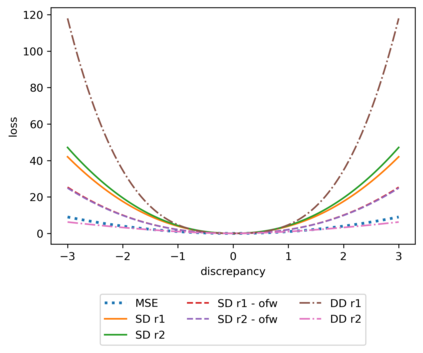
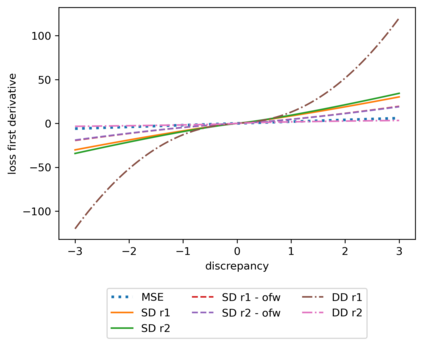
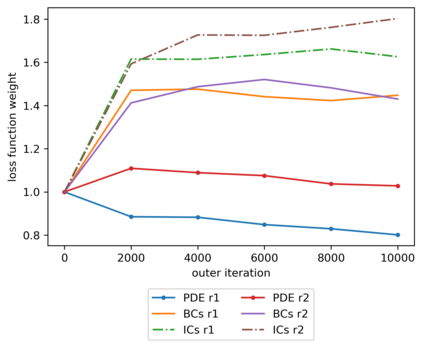
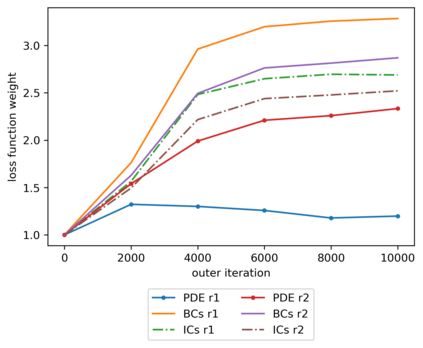
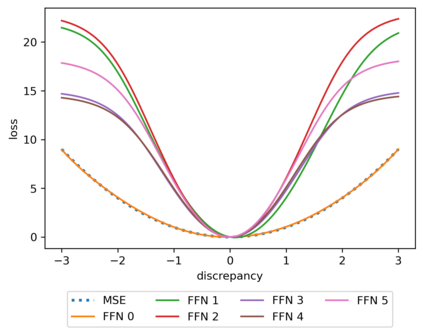
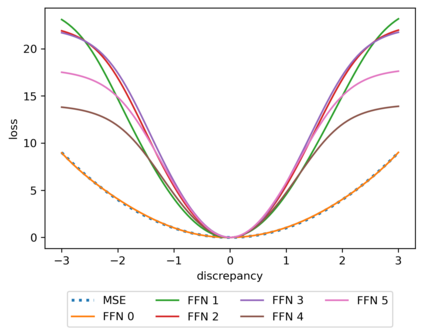
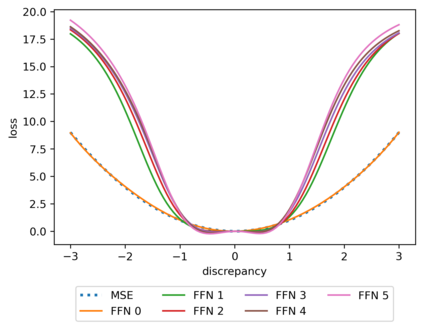
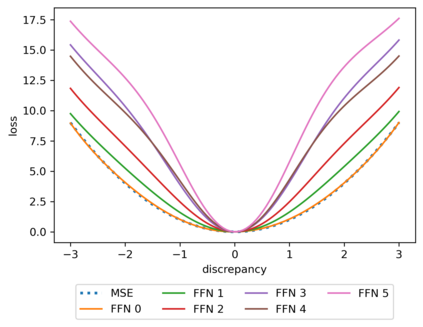
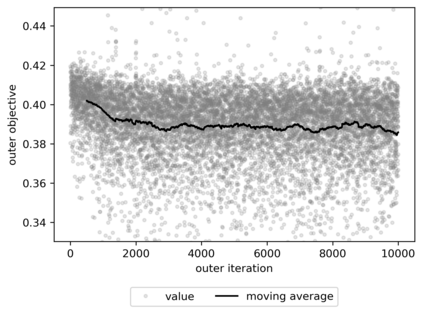
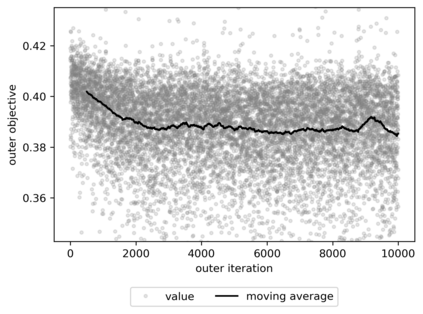
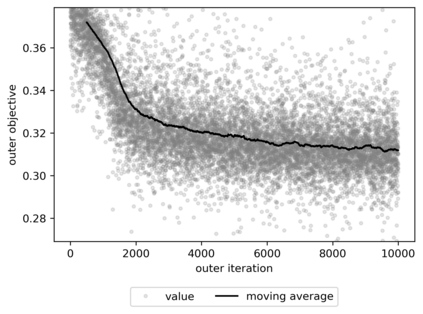
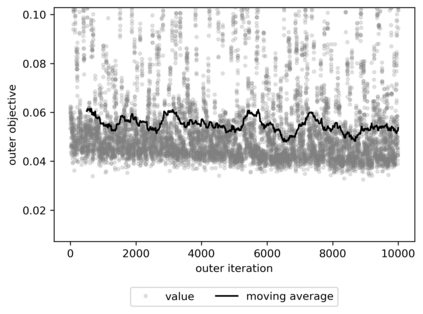
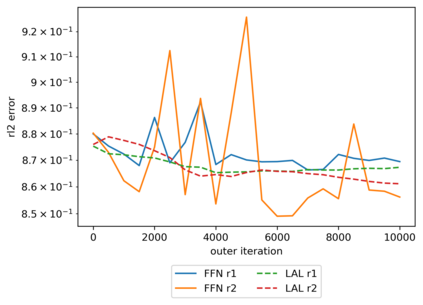
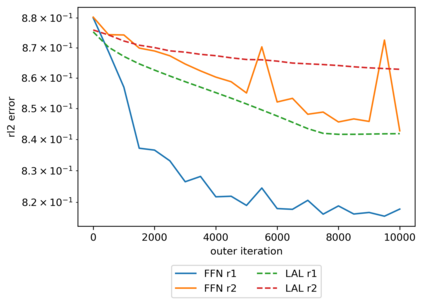
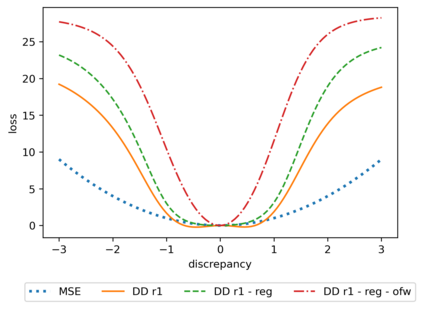
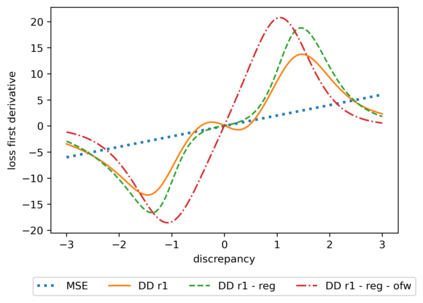
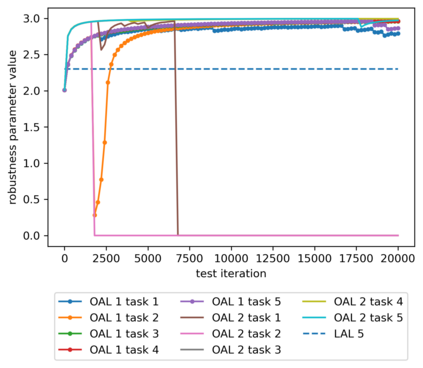
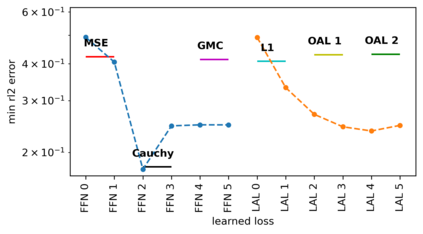
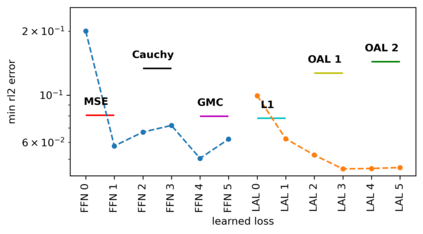
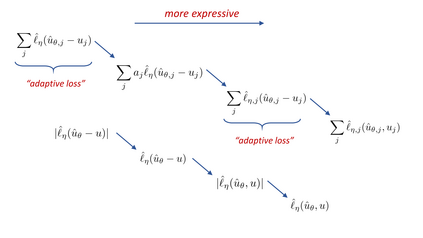
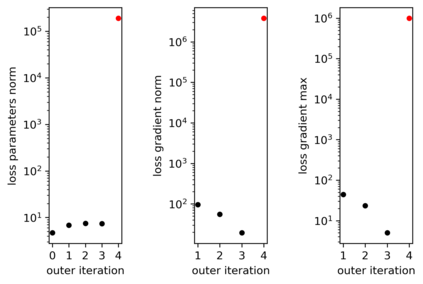
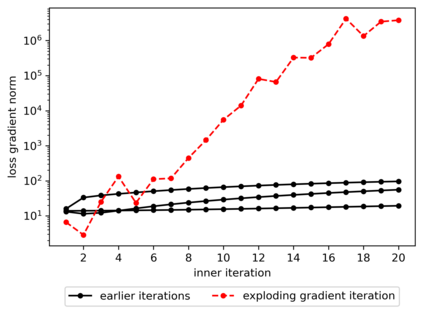
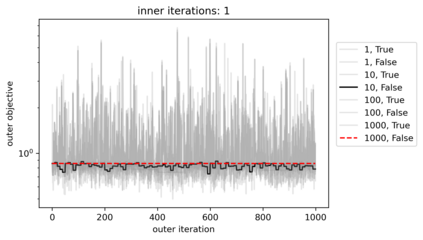
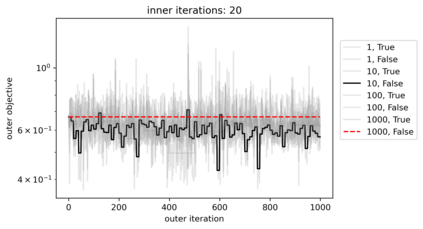
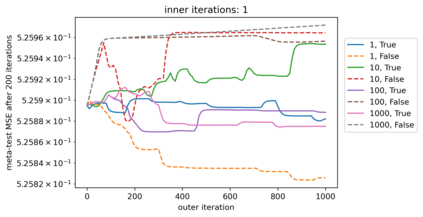
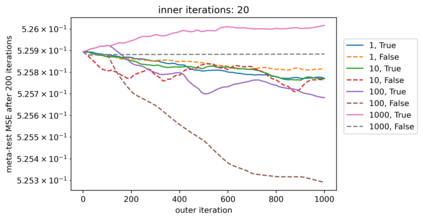
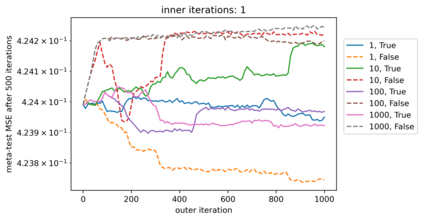
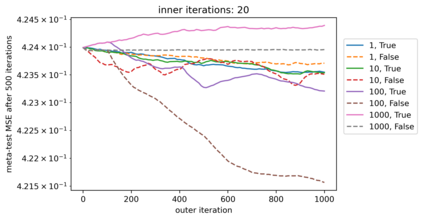
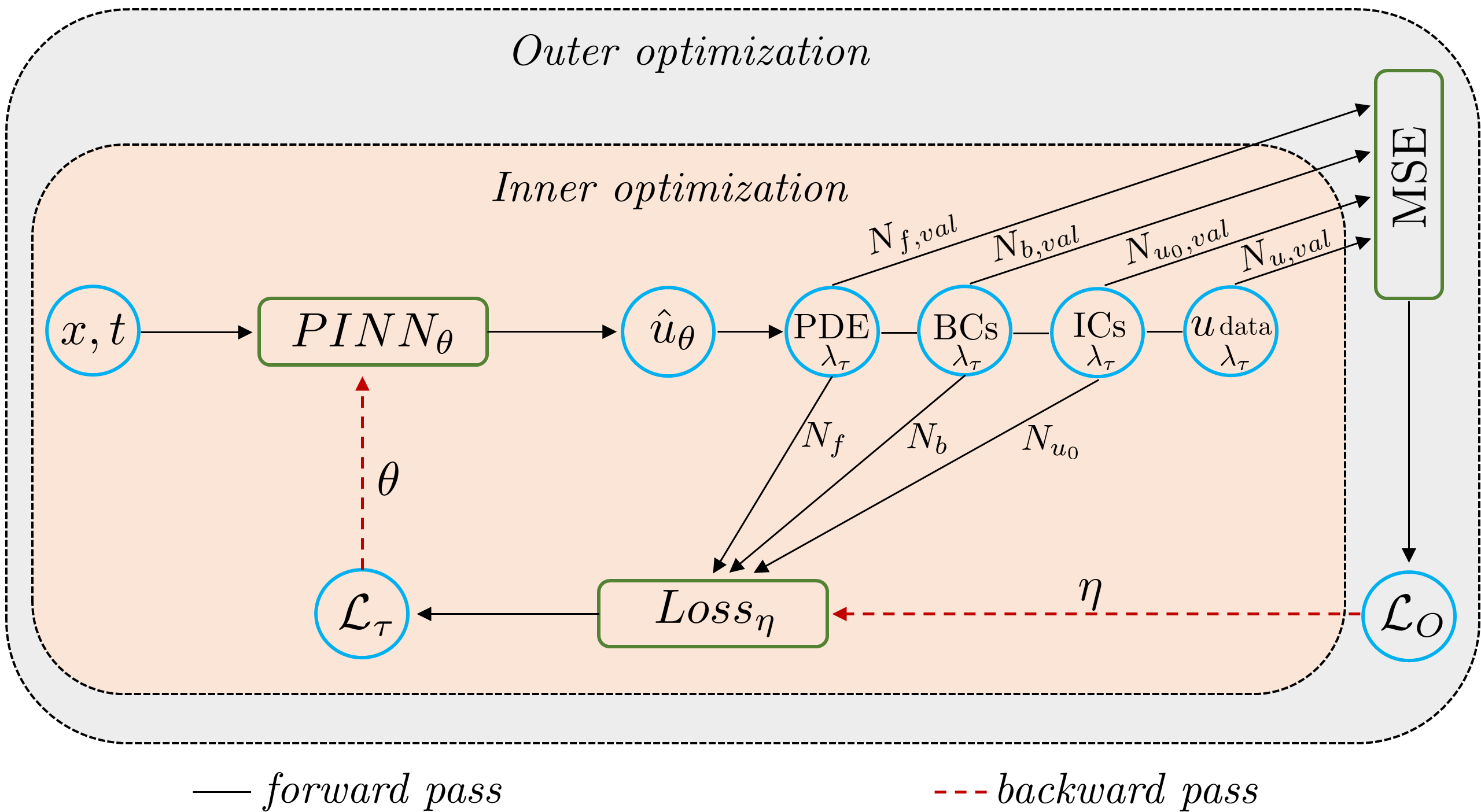
We propose a meta-learning technique for offline discovery of physics-informed neural network (PINN) loss functions. We extend earlier works on meta-learning, and develop a gradient-based meta-learning algorithm for addressing diverse task distributions based on parametrized partial differential equations (PDEs) that are solved with PINNs. Furthermore, based on new theory we identify two desirable properties of meta-learned losses in PINN problems, which we enforce by proposing a new regularization method or using a specific parametrization of the loss function. In the computational examples, the meta-learned losses are employed at test time for addressing regression and PDE task distributions. Our results indicate that significant performance improvement can be achieved by using a shared-among-tasks offline-learned loss function even for out-of-distribution meta-testing. In this case, we solve for test tasks that do not belong to the task distribution used in meta-training, and we also employ PINN architectures that are different from the PINN architecture used in meta-training. To better understand the capabilities and limitations of the proposed method, we consider various parametrizations of the loss function and describe different algorithm design options and how they may affect meta-learning performance.
翻译:我们建议了一种脱线发现物理知情神经网络损失功能的元学习技术。我们扩大了早期的元学习工程,并开发了一种基于梯度的元学习算法,用于在与 PINN 一起解决的基于超美化部分差异方程式(PDEs)的不同任务分布。此外,根据新理论,我们确定了PINN问题中元收益损失的两种可取属性,我们通过提出一种新的正规化方法或使用损失函数的具体准称来实施这些属性。在计算示例中,元所得损失用于测试时间处理回归和PDE任务分布。我们的结果表明,即使采用共享的超超超等等离线损失函数,也可以通过共享的超网外吸收损失函数实现显著的绩效改进。在本案中,我们解决了不属于元培训中所用任务分配的测试任务,我们还采用了与在元培训中使用的PINN结构不同的PINN结构。为了更好地了解拟议方法的能力和局限性,我们考虑各种参数和模型化如何影响不同的模型化设计功能和模型化。