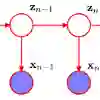
The hidden Markov model (HMM) is a classic modeling tool with a wide swath of applications. Its inception considered observations restricted to a finite alphabet, but it was quickly extended to multivariate continuous distributions. In this article, we further extend the HMM from mixtures of normal distributions in $d$-dimensional Euclidean space to general Gaussian measure mixtures in locally convex topological spaces. The main innovation is the use of the Onsager-Machlup functional as a proxy for the probability density function in infinite dimensional spaces. This allows for choice of a Cameron-Martin space suitable for a given application. We demonstrate the versatility of this methodology by applying it to simulated diffusion processes such as Brownian and fractional Brownian sample paths as well as the Ornstein-Uhlenbeck process. Our methodology is applied to the identification of sleep states from overnight polysomnography time series data with the aim of diagnosing Obstructive Sleep Apnea in pediatric patients. It is also applied to a series of annual cumulative snowfall curves from 1940 to 1990 in the city of Edmonton, Alberta.
翻译:隐藏的 Markov 模型( HMMM) 是一个典型的模型工具, 其应用范围很广。 其初始阶段考虑的观测仅局限于一个限定的字母, 但快速扩展为多变量连续分布。 在本条中, 我们进一步将HMM从以美元为维的 Euclidean 空间正常分布的混合物扩大到当地等离子表层空间的Gaussian普通测量混合物。 主要创新是使用Onsager- Machlup功能作为无限空间概率密度函数的代理。 这允许选择适合特定应用的 Cameron- Martin 空间。 我们通过将该方法应用于模拟扩散过程, 如布朗和分数布朗采样路径以及Ornstein- Uhlenbeck 进程, 显示了该方法的多功能性。 我们的方法用于从夜间聚苯乙烯时间序列中识别睡眠状态数据, 目的是对脑膜镜像病人的睡眠Apnea进行分辨。 这种方法还适用于1940- 1990 至 1990 年 月 的艾伯塔 市内一系列 。