ICLR2019 图上的对抗攻击

本文是一篇图上对抗攻击的实操论文.来自图对抗攻击大佬Stephan.

作者: 雪的味道(清华大学)

编辑: Houye

Graph Adversarial Attacks的一个里程碑，作者也是Nettack的作者，Nettack是kdd 2018获得了best paper。

图对抗攻击基础

见上一篇文章:「弱不禁风」的图神经网络

Abstract

本文核心是用meta-gradients去解决bilevel问题（投毒攻击需要在修改后的图上重训练，依然在测试集上结果下降，所以是一个bilevel的问题）。本文通过微小扰动，使得分类准确率比baseline降低很多，并且能够泛化到无监督的表示学习中。

Introduction

之前的工作基本是Targeted攻击，对指定点进行攻击使其误分类。比如：社交网络中某个人。这本文的工作中，首次提出一个降低模型的全局分类性能的算法。本质上，作者是把基于梯度的深度学习模型优化过程颠倒过来，把输入数据（图）当作一个超参数来学习。

Problem Formulation

GCN的学习过程可以用如下形式表达：

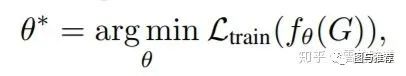
其中  是我们需要学习的参数，  是GCN模型。

Overall Goal

投毒攻击可以被表示为： 

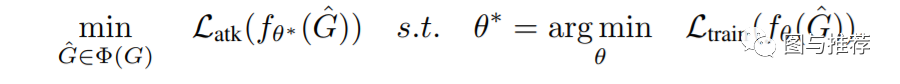
在全局攻击场景，攻击者试图降低模型泛化能力，降低在未标注的节点的上表现。

由于测试集节点的label未知，所以没有办法直接优化这个loss，所以作者提出了两种解决方案。一种是以降低训练集的loss为目标，此时  ，这种方式是假设训练集loss提高，那么测试集也跟着降低。实际这种方法并不合理，因为训练loss低可能是过拟合，提高训练loss未必会降低他的泛化能力，也可能刚好相反。另一种是用字学习的方式，先用gcn学习出test的结果，作为标签，然后此时可以  .

值得注意的是，如上的目标函数，是一个bilevel问题，而且更糟糕的是，图结构的邻接矩阵，每个元素只能是0或者1，所以这也是一个离散优化的问题。

Graph Structure Poisoning via Meta-Learning

Poisoning via Meta-Gradients

为了解决bilevel问题，本文采用meta-gradients的方法（这是在meta-learning领域常用的方法）。

Meta-gradients(比如每个超参数的梯度)是通过一个可微的模型（比如神经网络）反向传播得到的。本文的对抗攻击的核心idea就是把图结构的邻接矩阵当成超参数。在训练后，攻击者loss的梯度如下： 

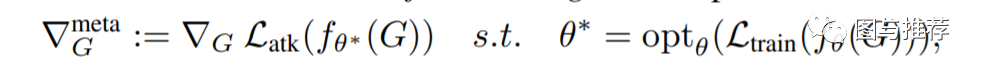
其中  操作是一个可微的优化操作。这个meta-gradients正式代表了攻击者的loss  在数据进行微小扰动后的训练后的改变程度，这正是投毒攻击者所需要了解的。

考虑我们设置优化函数  为原始的梯度下降，学习率为  ，可以写成如下形式： 

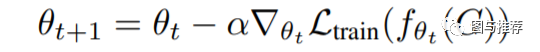
攻击者的loss在T次更新后为  ,则meta-gradient可以展开表示为如下形式： 

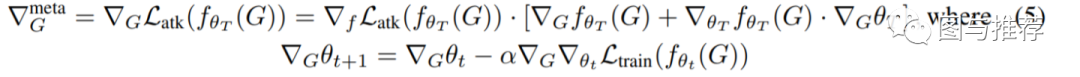
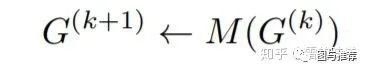
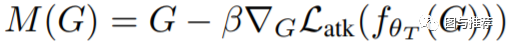
这个公式是一个复合函数求导，然后由于  是关于  的函数，所以是一个多元函数求导，其中  关于  的梯度可以分解迭代反推至初始化的参数  。我们定义用meta-gradients更新  去使  最小化的操作为  ： 

其中  为每次更新的步长大小。

但是值得注意的是，这里并没有解决图数据的离散性质，对于一个离散数据，梯度是不存在的，所以这里首先放款离散的条件，当成连续处理。但是在更新时，每次依然是离散的更新，下一节，提出一种贪心的方式保持数据的离散和稀疏性质。

Greedy Poisoning Attacks Via Meta Gradinets

作者使用SGC作为代理模型（GCN之类的也行，SGC与GCN的差别在于没有中间的非线性，实际实验表现与GCN不相伯仲，但是由于没有非线性，速度快了非常的多）。形式如下： 

接着这一段符号太多，我还是截图上原文吧。 

大概意思就是搞个评分矩阵  ，这玩意是邻接觉真的梯度的一个变型，这样这个值就可以直接对应于是否加边减边的score，这样我们就能选一个梯度最大的作为需要改变的边。

Experiments

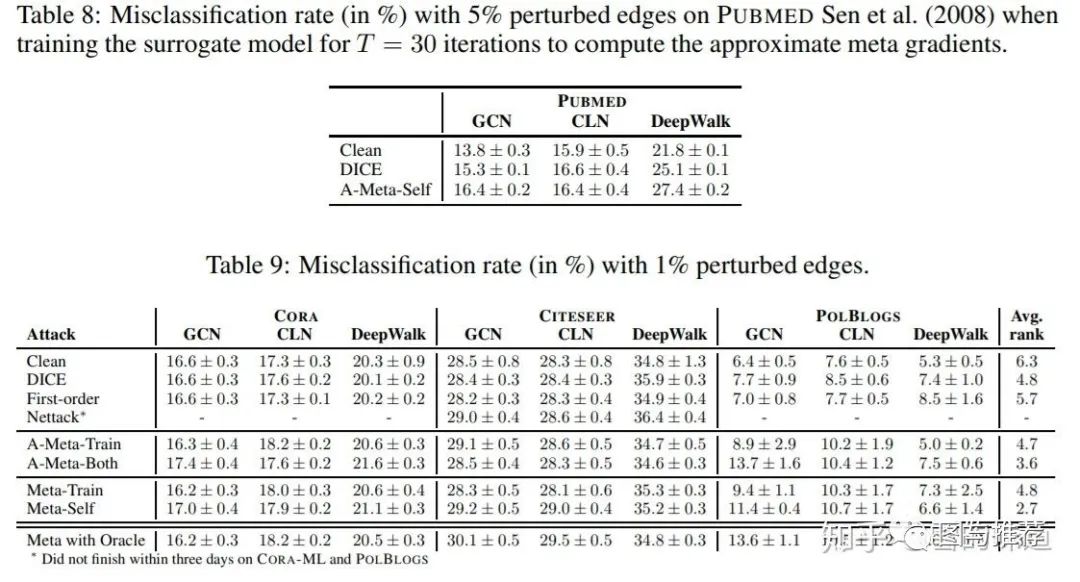
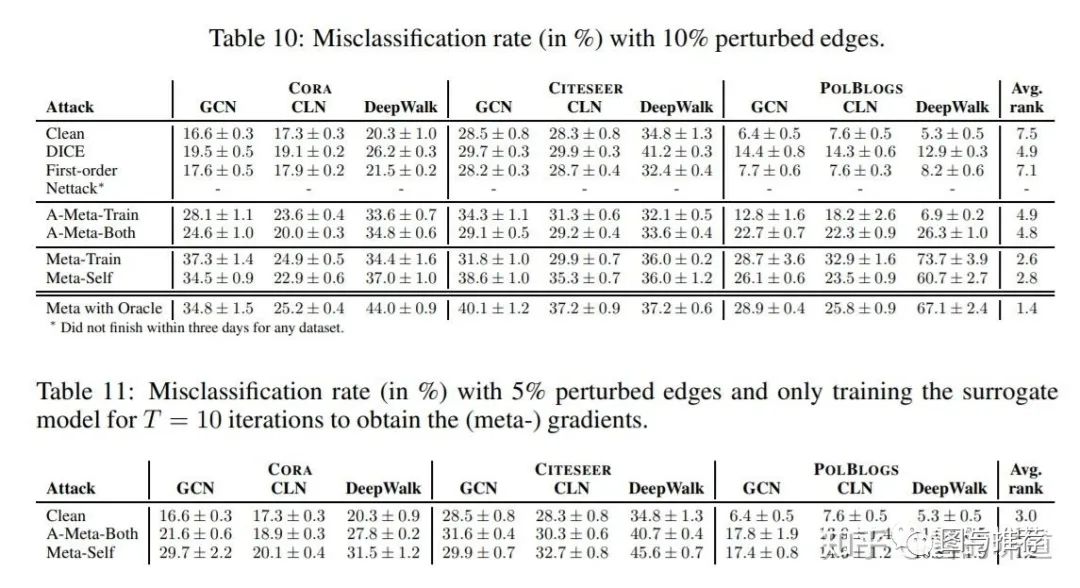
Impact of graph structure and trained weights

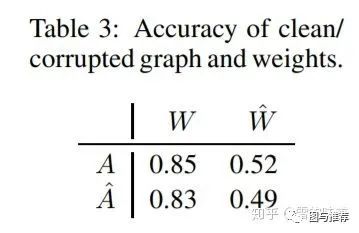
作者实验发现，如果使用干净图训练得到的参数，那么即使在被攻击的图上测试，效果仅仅略有下降。而用被攻击的图训练的参数，即使在干净图上做预测，结果依然大幅度下降。

Analysis of attacks

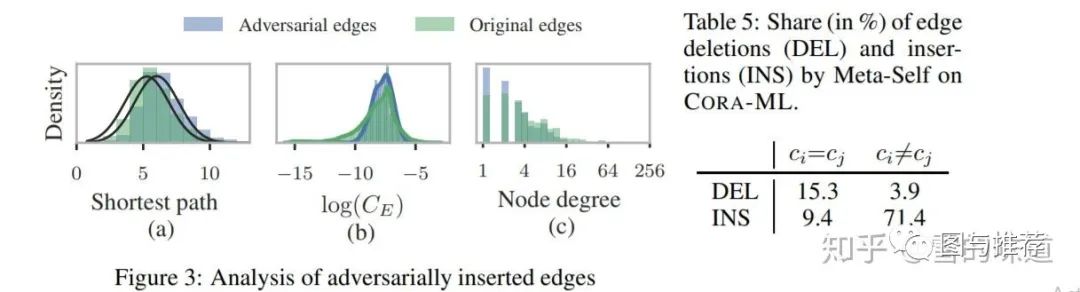
这一模块是分析为啥攻击有效。直接放结论，大概就是节点对间最短路径变长一些，不确定性增加，度分布更偏低（这里很疑惑，原本我认为是应该度分布变高，不知道是我理解错了还是作者画反了），但是整体分布与原图大体保持一致。图上大部分是加边，少部分删边，加边大部分两个节点是不同的label，而删除的大多数是相同label。

Limited knowledge about graph struceture

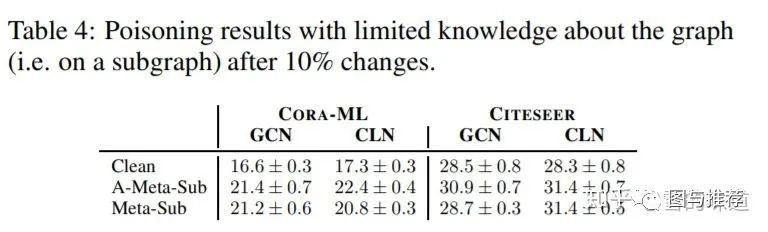
inductive learning的场景，metalearning依然有效。