数学建模9：数据直径、荣格定理及凸集

本讲导读

       凸分析是数学新课标中新加入的内容，不仅在信息技术中有非常重要的应用，也为很多古典数学问题提供了异常优雅的解决方式。

       本讲适合在讲授或学习完高中数学的集合章节、解三角形章节、平面解析几何章节、数学归纳法章节后，作为数学建模材料，在日常教学中讲授或学习，本讲内容包括但不限于：

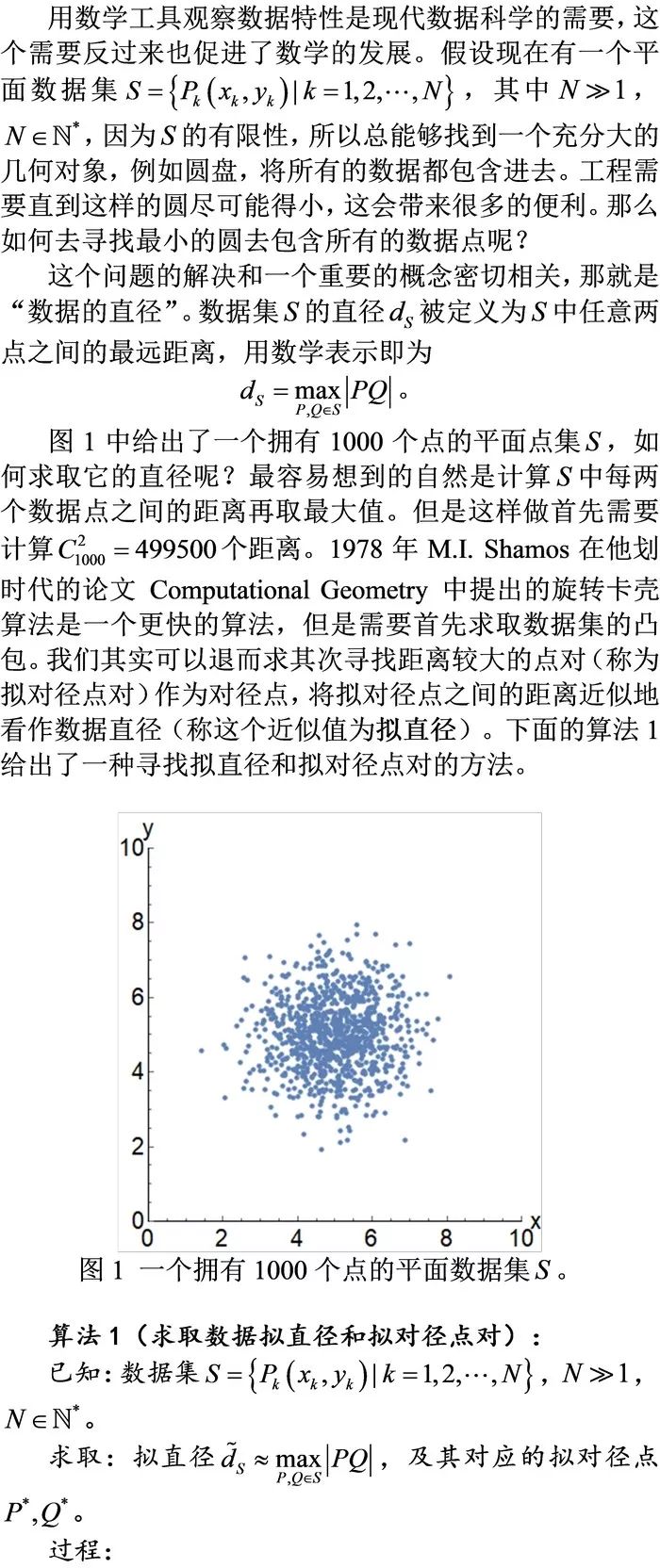
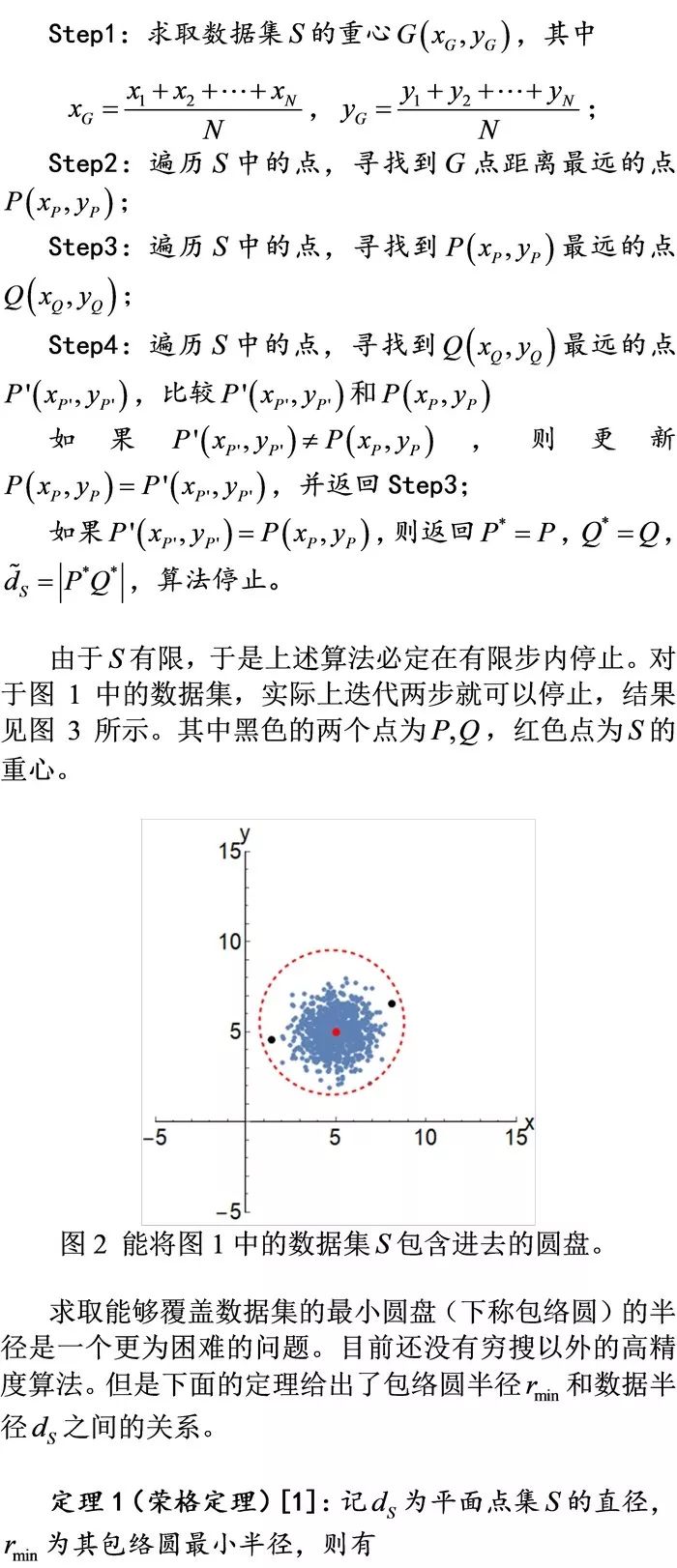
       1. 数据直径及包络圆；

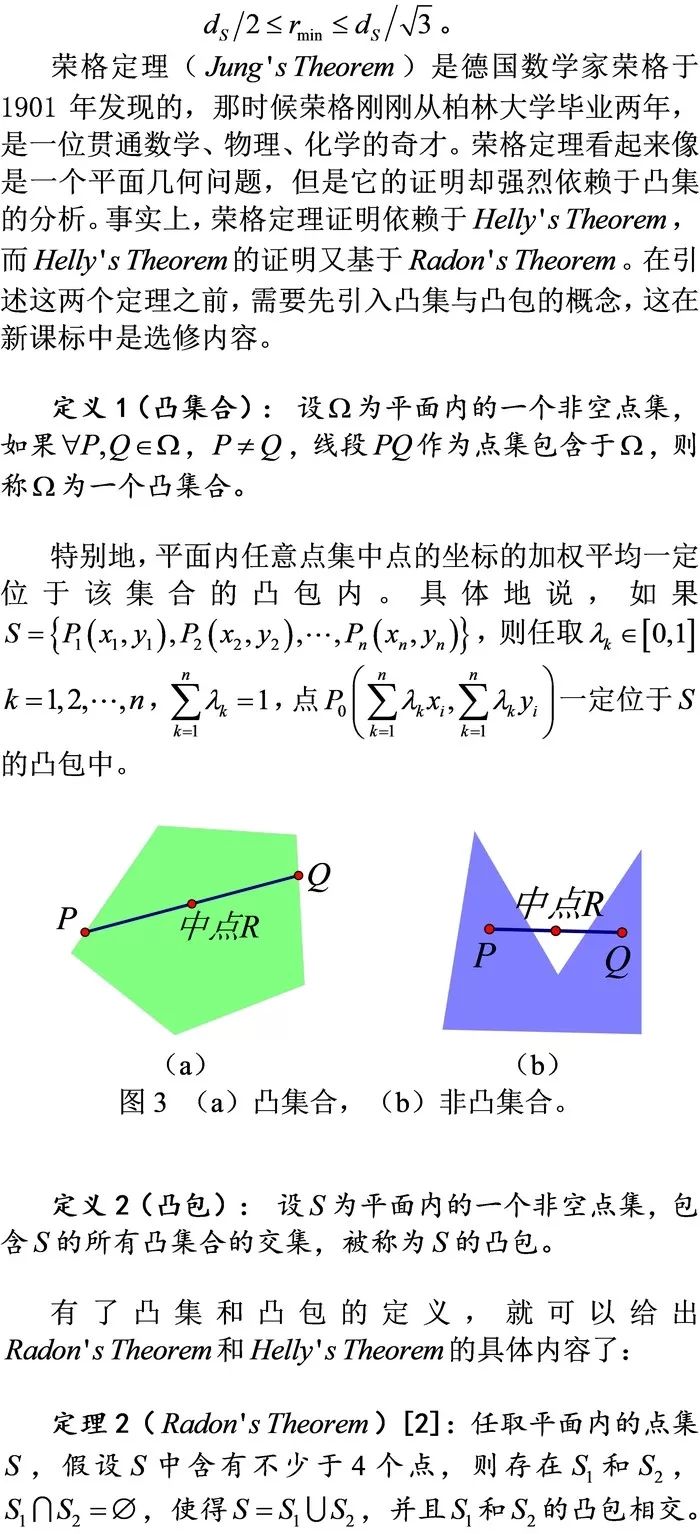
       2. 二维（平面内）荣格定理及其证明，凸集合与凸包；

       3. Radon's Theorem 和 Helly's Theorem；

       4. 一般维度下的荣格定理；

       5. 荣格定理的应用——估计数据直径。

参考文献：

[1] Arseniy V. Akopyan, CombinatorialGeneralizations of Jung’s Theorem[J], Discrete Computational Geometry (2013)49:478–484.

在线浏览及下载地址：https://www.mccme.ru/~akopyan/papers/Akopyan-Jung.pdf.

[2] Radon's theorem, https://en.wikipedia.org/wiki/Radon%27s_theorem,2019.3.29, 13:36.

[3] Helly's theorem, https://en.wikipedia.org/wiki/Helly%27s_theorem,2019.3.29, 13:36.

日常生活中的数学建模系列文章：

» 日常生活 01: 日常生活中的等差数列和等比数列

» 日常生活 02: 二次和三次函数样条、数据的插值

» 日常生活 03: 指数函数与对数函数的普适价值

» 日常生活 04: 三角函数与极小曲面

» 日常生活 05: 概率的加法与乘法原理、加权平均的递推

» 日常生活 06: 解析几何与带标签数据的模糊线性分类

» 日常生活 07: 进制观点下的分类、距离与解析

» 日常生活 08: 迭代预测的测不准原理与熵距