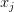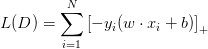Python · SVM（三）· 核方法

Python.SVM(三）核方法

1

什么是核方法

往简单里说，核方法是将一个低维的线性不可分的数据映射到一个高维的空间、并期望映射后的数据在高维空间里是线性可分的。

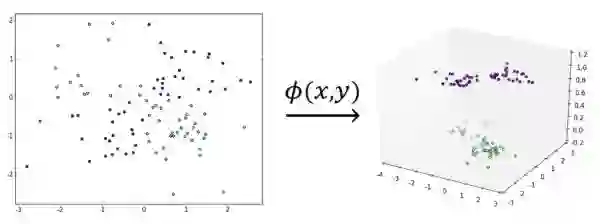
我们以异或数据集为例：在二维空间中、异或数据集是线性不可分的；但是通过将其映射到三维空间、我们可以非常简单地让其在三维空间中变得线性可分。

比如定义映射：

该映射的效果如下图所示：

可以看到，虽然左图的数据集线性不可分、但显然右图的数据集是线性可分的，这就是核工作原理的一个不太严谨但仍然合理的解释

从直观上来说，确实容易想象、同一份数据在越高维的空间中越有可能线性可分，但从理论上是否确实如此呢？

1965 年提出的 Cover 定理从理论上解决了这个问题，我们会在文末附上相应的公式，这里暂时按下不表

至此，似乎问题就转化为了如何寻找合适的映射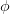、使得数据集在被它映射到高维空间后变得线性可分。

不过可以想象的是，现实任务中的数据集要比上文我们拿来举例的异或数据集要复杂得多、直接构造一个恰当的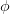的难度甚至可能高于解决问题本身。

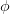
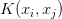
而核方法的巧妙之处就在于，它能将构造映射这个过程再次进行转化、从而使得问题变得简易：它通过核函数来避免显式定义映射往简单里说，核方法会通过用能够表示成的核函数替换各算式中出现的内积来完成将数据从低维映射到高维的过程。

换句话说、核方法的思想如下：

• 将算法表述成样本点内积的组合（这经常能通过算法的对偶形式实现）

• 设法找到核函数，它能返回样本点、被作用后的内积

  
  

• 用替换、完成低维到高维的映射（同时也完成了从线性算法到非线性算法的转换）

当然了，不难想象的是，并不是所有的函数都能够对应一个映射（亦即不是所有的都能拆成比如说，显然至少需要是一个对称函数）。

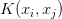
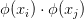
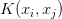
幸运的是，1909 年提出的 Mercer 定理解决了这个问题，它的具体叙述会在文末给出。

Mercer 定理为寻找核函数带来了极大的便利。可以证明如下两族函数都是核函数：

那么核方法的应用场景有哪些呢？在 2002 年由 Scholkopf 和 Smola 证明的表示定理告诉我们它的应用场景非常广泛。定理的具体内容同样会附在文末。

2

 核模型的表现

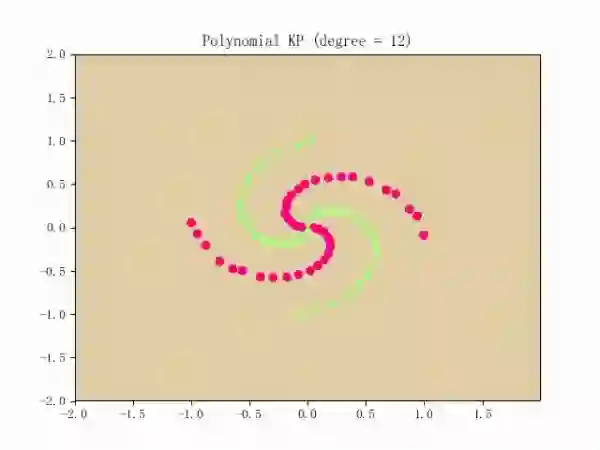
还是用 GIF 来说明问题最为形象。

当我们对感知机应用核方法后，它就能对非线性数据集（比如螺旋线数据集）进行分类了，训练过程将如下：

3

 

 怎么应用核方法

简单来说，就是把算法中涉及到样本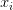的地方都通过某种变换、弄成样本的内积形式。以感知机为例，感知机的原始损失函数为：

转自：机器学习算法与自然语言处理