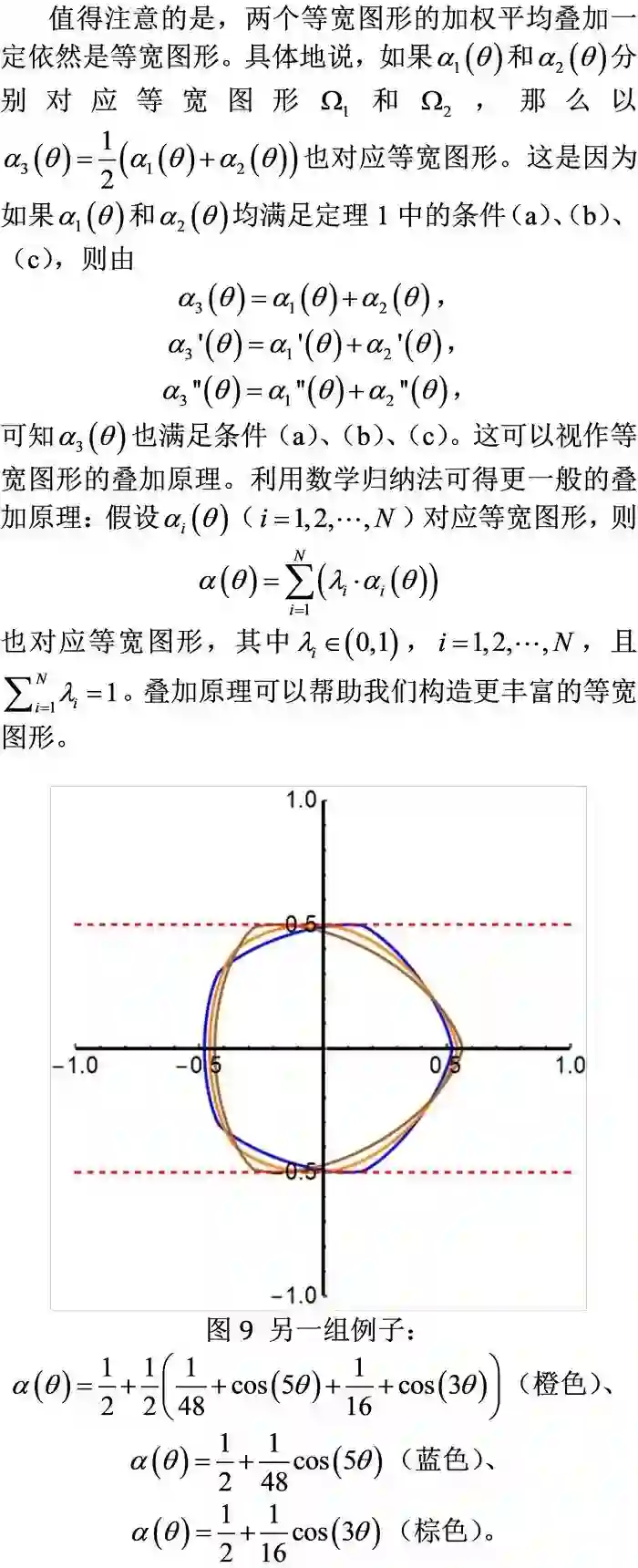
数学建模14：井盖、滚木与等宽图形，圆与勒洛三角形

本讲导读

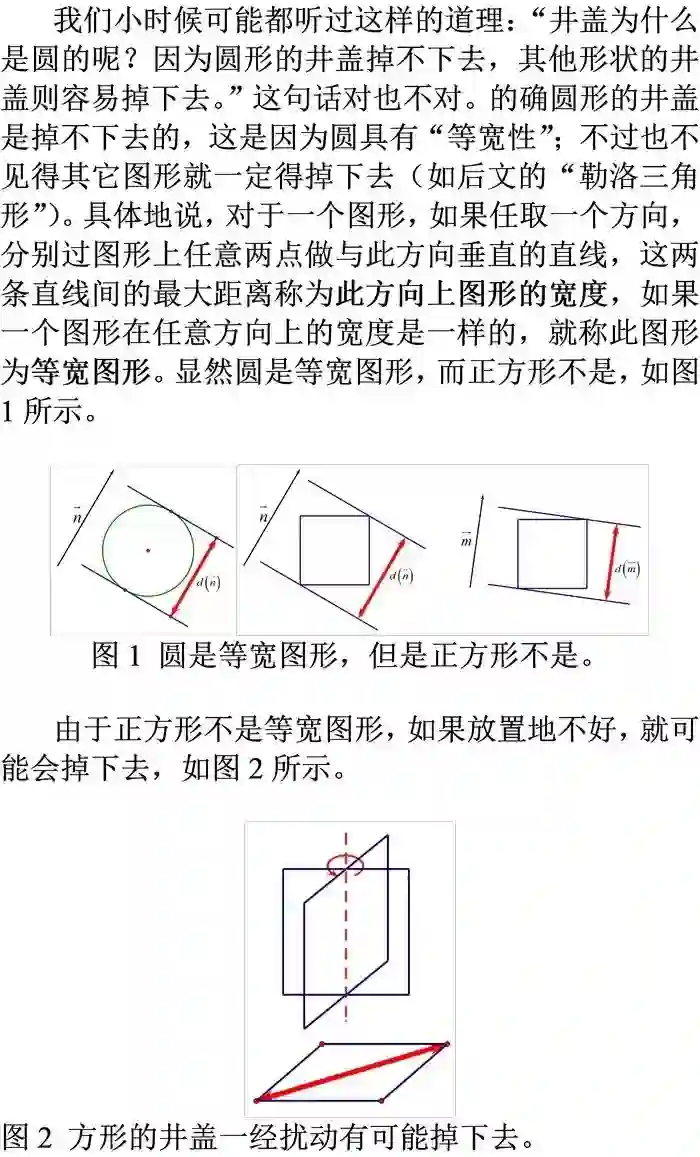
       有很多非常深刻的数学方法，都是根植于问题的解决策略中。日常生活中常见的井盖、造金字塔时所用的滚木搬运法，不仅蕴含着“等宽图形”这种概念，而且其典型的研究方法就是近代几何中非常重要的活动标架法——陈先生曾经用此方法给出了高斯-博纳公式的内蕴证明，本文将从更初等的角度，以平面上等宽图形这一生活中常用图形为载体，在高中知识范围内去解释活动标架法的奇妙作用。

       本讲适合在讲授或学习完高中数学的解析几何、平面向量、导数章节后，作为数学建模材料，在日常教学中讲授或学习。本讲内容包括但不限于：

       1.生活中的等宽图形；

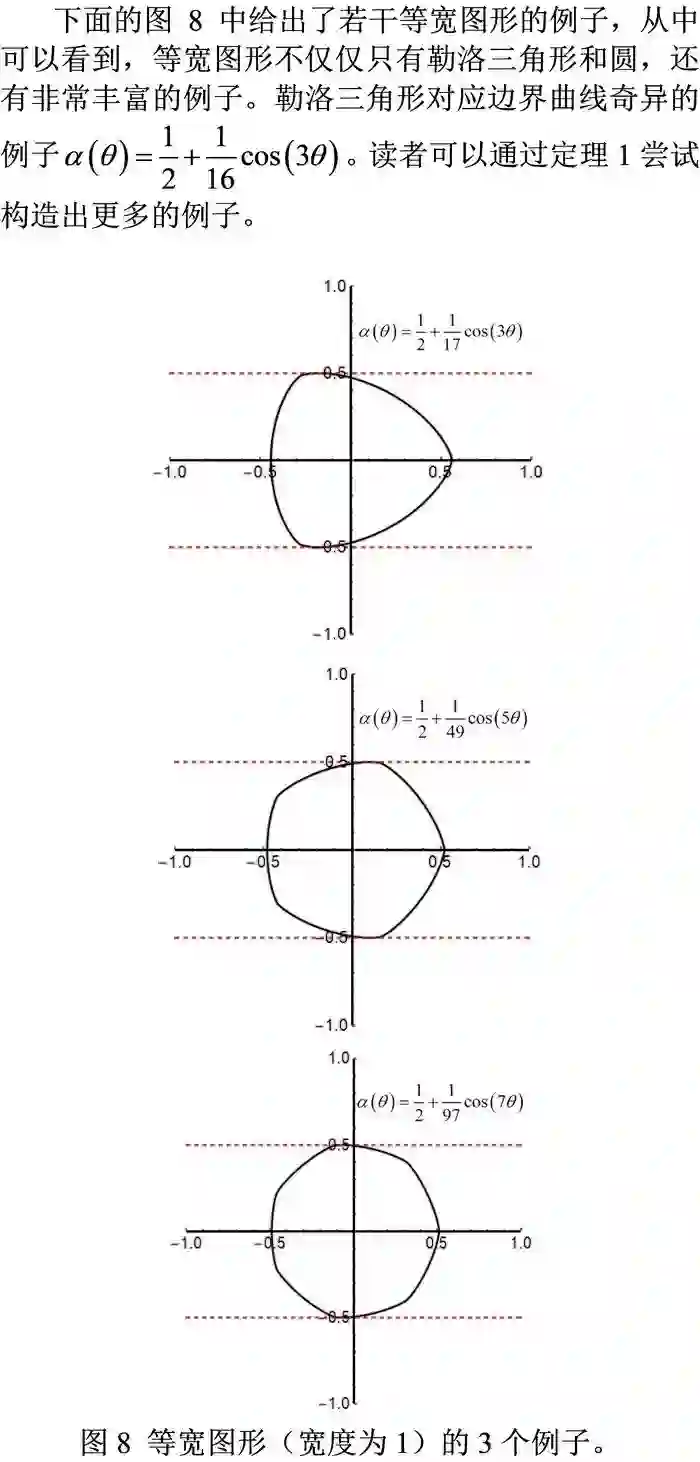
       2.勒洛三角形的构造及其性质；

       3.等宽图形的边界曲线方程及其性质；

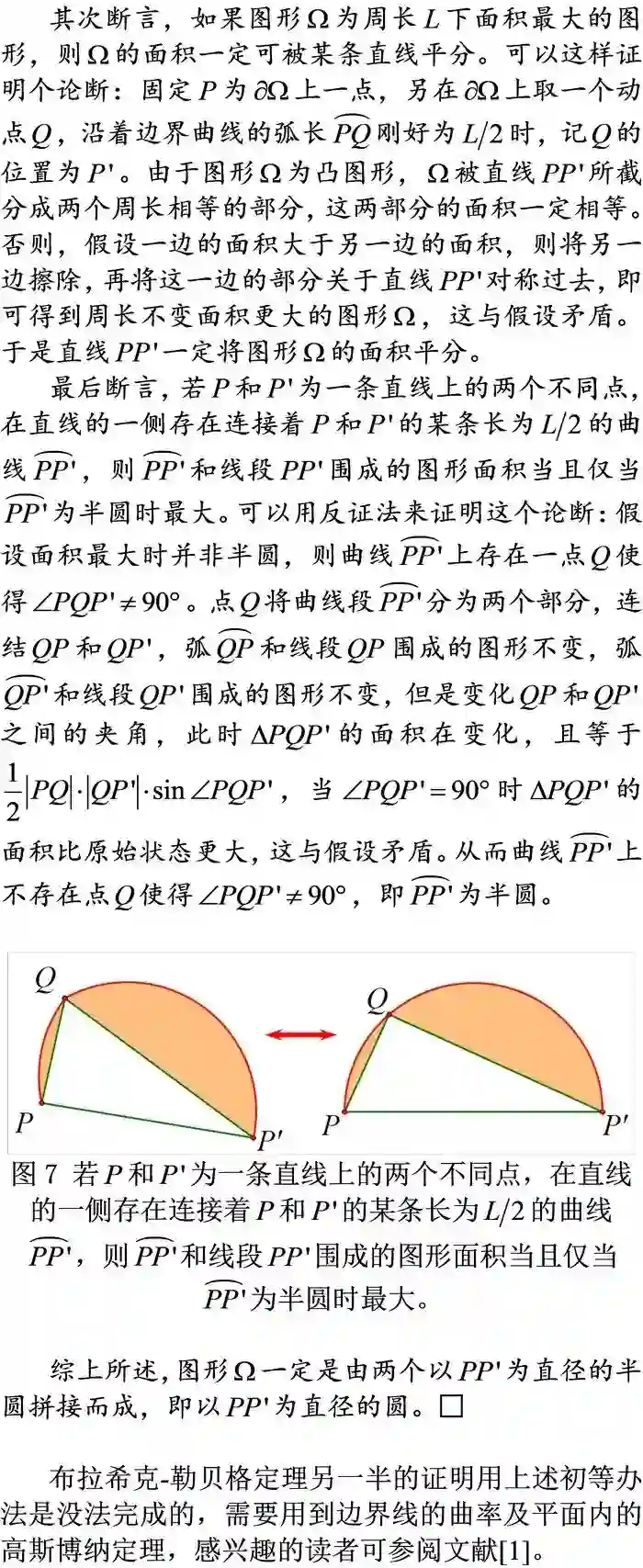
       4.等宽图形的面积、布拉希克-勒贝格定理一半结论的初等证明；

       5. 等宽图形的叠加原理。

参考文献及引申读物：

[1]Evans M. Harrell, A direct proof of a theorem of Blaschke and Lebesgue,arXiv:math/0009137 [math.MG], Thu, 14 Sep 2000.

在线阅读及下载地址：
http://people.math.gatech.edu/~harrell/Pubs/reul.pdf.

[2]Lucie Paciotti, Curves Of Constant Width And Their Shadows, May 14, 2010. 下载地址：
https://www.whitman.edu/Documents/Academics/Mathematics/SeniorProject_LuciaPaciotti.pdf.

日常生活中的数学建模系列文章：

» 01: 日常生活中的等差数列和等比数列

» 02: 二次和三次函数样条、数据的插值

» 03: 指数函数与对数函数的普适价值

» 04: 三角函数与极小曲面

» 05: 概率的加法与乘法原理、加权平均的递推

» 06: 解析几何与带标签数据的模糊线性分类

» 07: 进制观点下的分类、距离与解析

» 08: 迭代预测的测不准原理与熵距

» 09: 数据直径、荣格定理及凸集

» 10: 欧式与离散几何的桥梁——皮克定理及其应用

» 11: 暗室与艺廊——平面几何与照明

» 12: 纽结与琼斯多项式

» 13: 同余与随机数生成器